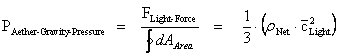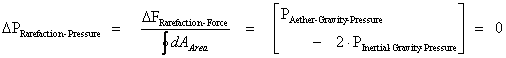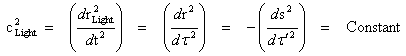What is the Cosmic Censorship Hypothesis?
What are Black Hole Physical and Naked Singularities?
By
Robert Louis Kemp
Super Principia Mathematica
The Rage to Master Conceptual & Mathematical Physics
www.SuperPrincipia.com
www.Blog.Superprincipia.com
Flying Car Publishing Company
P.O Box 91861
Long Beach, CA 90809
Abstract
A question that the physics community is asking today, is, “What is a Singularity?”, and “Are Singularities Detectable and Measurable?” This work, will describe five (5) different types or classifications of “Singularities” in nature: the Inverse Distance Power Law Singularity, the Physical Singularity, the Naked Singularity, the Coordinate Singularity, and the Big Bang Singularity. Correlating the nature of these singularities, with the mathematics, theory, and the real physical world, is a conundrum in physics.
This work extends the “Strong and Weak Cosmic Censorship” hypotheses originally proposed an debated by Roger Penrose, Steven Hawking, and Kip Thorne, by adding an additional thirteen (13) “Censorships” which removes some of the contradiction that exists with just the two (2) original “Cosmic Censorship Hypotheses” alone. The “Penrose–Hawking–Thorne” singularity theorems, of General Relativity Theory, described in this work, addresses mathematically the concept of “Geodesic Incompleteness”; which is another name for a geodesic with infinite curvature, which at one end of the geodesic is a singularity. And “Geodesic Completeness” another name for a geodesic with infinite curvature, on a 2-Sphere Riemann Manifold; there the Non-Euclidean geometry still predicts a singularity.
PDF![pdf[1]](https://superprincipia.files.wordpress.com/2012/11/pdf1.gif?w=16&h=16) – The What is the Cosmic Censorship Hypothesis? What are Black Hole Physical and Naked Singularities?
– The What is the Cosmic Censorship Hypothesis? What are Black Hole Physical and Naked Singularities?
Keywords: General Relativity, Einstein Field Equation, Gravitational Field, Coordinate Singularity, Physical Singularity, Gravitation, Black Hole Event Horizon, Spherically Symmetric Metric, Euclidean Geometry, Non-Euclidean Geometry, Minkowski Metric, Einstein Metric, Schwarzschild Metric, Kruskal-Szekeres Metric, Inverse Distance Power Law, Singularities, Hyperbolically Symmetric Metric, Cosmic Censorship Hypothesis, Naked Singularity, Big Bang, Geodesic Incompleteness, Geodesic Completeness
Contents
· 1.0 Introduction – What are Singularities
· 1.1 Inverse Distance Power Law Singularities
· 1.2 Non-Euclidean – Spherically Symmetric – Schwarzschild Metric and the “Physical Singularity”
· 1.3 Non-Euclidean – Hyperbolically Symmetric – Kruskal-Szekeres Metric and the “Naked Singularity”
· 1.4 Big Bang Singularity
· 1.5 Cosmic Censorship Hypothesis
· 1.6 Gravitational Field and Electrostatic Field Inverse Power Laws and Singularities
· 1.7 Spherically Symmetric Metric – Limits of Integration – Euclidean & Pseudo-Euclidean Minkowski Metrics
· 1.8 Spherically Symmetric Metric – Limits of Integration & “Physical” Singularities – Schwarzschild Non-Euclidean Metric
· 1.9 Hyperbolic Symmetric Metric – Limits of Integration & “Naked” Singularities – Kruskal-Szekeres Non-Euclidean Metric
· 1.10 Geodesic Incompleteness
· 1.11 Geodesic Completeness, Null Geodesics, & Space-Time Manifolds
· 1.12 Non-Euclidean Metrics & Inverse Distance Power Law Conundrum
· 1.13 Extended Cosmic Censorship Hypothesis
· 2.0 Conclusion
· 3.0 Appendix – 1 ─ Original Bet on Naked Singularities: Stephen W. Hawking, John P. Preskill, Kip S. Thorne
· 4.0 Appendix – 2 ─ New Bet on Naked Singularities: Stephen W. Hawking, John P. Preskill, Kip S. Thorne
· 5.0 Appendix – 3 ─ Table of Cosmic Censorship Hypotheses and the Author’s Viewpoint
· 6.0 Appendix – 4 ─ Table of Universal Constants
1. Introduction – What Are Singularities of Matter?
A question that a lot of physicists ask today, is, “What is a Singularity?”, and “Are Singularities Detectable and Measurable?” This work, will attempt to describe three different types or classifications of “Singularities” in nature.
In more recent day publishing and literature, there are many different names given to these “singularities”. This work will attempt to conceptualize and organize these different concepts of “singularities” in a way that could be discussed as a subject.
The ground work and foundation for conceptualizing by hypothesis the different types of “singularities” which could be found in nature, was laid down by: Roger Penrose (1969), Stephen Hawking (1970), and Kip Thorne (1991); with their “Strong Cosmic Censorship” and “Weak Cosmic Censorship” hypotheses.
This work extends the “Cosmic Censorship” by adding additional “Censorships” which removes some of the contradiction that exists with just the two (2) “Cosmic Censorship Hypotheses” alone.
The general concept of a “Singularity” in physics and mathematics, describes a point in a space, time, gravitational field, or electrostatic field at which a given physical parameter is not defined.
A more conceptually rigorous definition of a “Singularity”, is a point of an “exceptional set” of values, that when input to a mathematical object, fails to be well-behaved, in some particular way, relative to other points in the output of the mathematical object, which are well-behaved.
In this work, the only “exceptional set” of input values that will be considered, for the mathematical objects, are the set of space points which range from zero distance (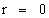 ) which originates in a center, out to an infinite distance (
) which originates in a center, out to an infinite distance (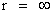 ) away from a center; (
) away from a center; (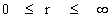 ).
).
The most common types of “Singularities” that will be described in this work, and that which is discussed in physics today, independent of what caused them, or their purpose, are the following:
· Inverse Distance Power Law ─ Singularities
· Black Hole Physical, Coordinate & Naked Singularities
· Big Bang ─ Singularity
1.1. Inverse Distance Power Law Singularities
The “Inverse Distance Power Law – Singularities” commonly show up in the physics of the Newtonian Gravitational Force Law (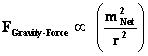 ) and the Gaussian Electrostatics Force Law. (
) and the Gaussian Electrostatics Force Law. (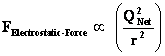 ); whose values depend on the inverse square of the distance “power law”, relative to the origins or center of the gradient “Gravitational Field” or gradient “Electrostatic Field” system body; where (
); whose values depend on the inverse square of the distance “power law”, relative to the origins or center of the gradient “Gravitational Field” or gradient “Electrostatic Field” system body; where ( ).
).
And likewise the Inertial Mass Density (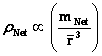 ) and the Electrical Charge Density (
) and the Electrical Charge Density (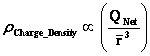 ) of matter, equations among other physical parameters such as: Lineal Density, Pressure, and Potential Energy, all have “Inverse Distance Power Law – Singularities” at the origins or centers (
) of matter, equations among other physical parameters such as: Lineal Density, Pressure, and Potential Energy, all have “Inverse Distance Power Law – Singularities” at the origins or centers (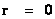 ) of the gradient “Gravitational Field” or gradient “Electrostatic Field”, of an isolated and conserved, mass or charged system body.
) of the gradient “Gravitational Field” or gradient “Electrostatic Field”, of an isolated and conserved, mass or charged system body.
Inverse Distance Power Law
1.1
( 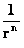 ) ;
) ; 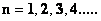
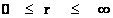
|
Inverse Distance Power Law
( 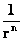 ) )
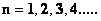
|
Spherically Symmetric Semi-Major Radius (Distance/Space)
(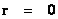 ) )
|
Spherically Symmetric Semi-Major Radius (Distance/Space)
(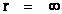 ) )
|
|
Inverse Distance Power Law
( 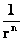 ) )
|

Infinitely Large Value
“Bang Singularity”
|

Infinitely Small Value
“Negligible Influence”
|
Where the exponent (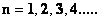 ), of the Inverse Distance Power Law, denotes the dimension of the space or space-time.
), of the Inverse Distance Power Law, denotes the dimension of the space or space-time.
The “Inverse Distance Power Law” ( ), predicts that every mass or charge is bound between two extremes, a zero and a singularity.
), predicts that every mass or charge is bound between two extremes, a zero and a singularity.
The “Inverse Distance Power Law” predicts “Infinitely Large”, value “Singularities” at the origin or center (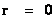 ), of any “gravitational field” or “electrostatic field” (
), of any “gravitational field” or “electrostatic field” ( ) isolated and conserved system.
) isolated and conserved system.
And likewise, on the extreme opposite distance spectrum, The “Inverse Distance Power Law” predicts “Infinitely Small”, “Zero”, or “Negligible” values at an infinite distance (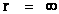 ) away from the center of any “gravitational field” or “electrostatic field” (
) away from the center of any “gravitational field” or “electrostatic field” ( ) isolated and conserved system.
) isolated and conserved system.
These “Inverse Distance Power Law – Singularities” ( ), are an example of the mathematical difficulty, of the concept of divergence to infinite Density, Force, Pressure, and Potential Energy, which reveals a profound problem in our understanding of the physics phenomena, that takes place at the, center (
), are an example of the mathematical difficulty, of the concept of divergence to infinite Density, Force, Pressure, and Potential Energy, which reveals a profound problem in our understanding of the physics phenomena, that takes place at the, center (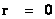 ) of an isolated and conserved system.
) of an isolated and conserved system.
Many in the physics community think that a workable theory of quantum gravity should be able to solve “singularity” problems such as these. I disagree, and believe that “Inverse Distance Power Law – Singularities” ( ) are an artifact of nature that we will always have to deal with. Not to mention, singularities have absolutely no effect on the mass in motion of any body, relative to any other body in the universe.
) are an artifact of nature that we will always have to deal with. Not to mention, singularities have absolutely no effect on the mass in motion of any body, relative to any other body in the universe.
I don’t know of any mathematical way, in which to remove or eliminate a singularity from the center of a system, which obeys any form of the Inverse Distance Power Law!
Keep in mind that Singularities do not in any way, effect the motion or behavior of mass or charged particles in our natural world! A singularity is more a problem of the way that we deal with the infinites that show up in our mathematics, than it is a problem of nature, which has to be solved.
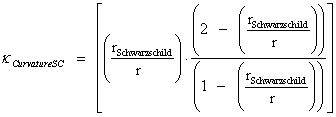
1.2. Non-Euclidean – Spherically Symmetric – Schwarzschild Metric and the “Physical Singularity”
In General Relativity, a “Physical Singularity” is manifest in the predictions of the Non-Euclidean Spherically Symmetric “Schwarzschild” Metric (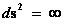 ), whenever there is an input of radius equals to zero (
), whenever there is an input of radius equals to zero (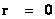 ) into the equation.
) into the equation.
The Non-Euclidean Spherically Symmetric “Schwarzschild” Metric (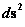 ) is an equation that describes a “geodesic” world “line element” (
) is an equation that describes a “geodesic” world “line element” (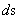 ), as a real curving or warping of physical space, space-time, or a gradient gravitational field, that is spherically symmetric, surrounding a condensed matter, mass (
), as a real curving or warping of physical space, space-time, or a gradient gravitational field, that is spherically symmetric, surrounding a condensed matter, mass (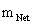 ), or energy source.
), or energy source.
The Schwarzschild Metric (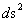 ) is a mathematical equation which describes a “geodesic” world “line element” (
) is a mathematical equation which describes a “geodesic” world “line element” (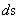 ), of a Riemannian manifold with spherically symmetric curvature of space-time, in the “presence” of matter or the Net (
), of a Riemannian manifold with spherically symmetric curvature of space-time, in the “presence” of matter or the Net (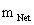 ) Mass, of a localized gradient gravitational field; whose space-time geodesic extends from a “Physical Singularity” at radius equals zero (
) Mass, of a localized gradient gravitational field; whose space-time geodesic extends from a “Physical Singularity” at radius equals zero (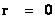 ), then extends to the surface of the Black Hole radius (
), then extends to the surface of the Black Hole radius (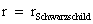 ) and finally into infinite (
) and finally into infinite (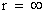 ) distances of that localized space-time gravity field.
) distances of that localized space-time gravity field.
The Schwarzschild Metric (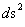 ) predicts that there is a Black Hole Event Horizon with two (2) “extreme curvature” singularities located at radius equals to zero (
) predicts that there is a Black Hole Event Horizon with two (2) “extreme curvature” singularities located at radius equals to zero (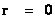 ), and the Schwarzschild Radius (
), and the Schwarzschild Radius (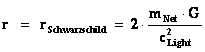 ) of the Black Hole Event Horizon.
) of the Black Hole Event Horizon.
For the Schwarzschild Metric (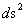 ) there is a “Black Hole” and a “Physical Singularity” (
) there is a “Black Hole” and a “Physical Singularity” (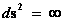 ), with an infinitely “small value”, located at the origin, or center (
), with an infinitely “small value”, located at the origin, or center (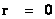 ) for every “Black Hole”, “gravitational field”, or “electrostatic field”, isolated and conserved system.
) for every “Black Hole”, “gravitational field”, or “electrostatic field”, isolated and conserved system.
And likewise there is a “Coordinate Singularity” ( ), located at the Black Hole Event Horizon Schwarzschild Radius (
), located at the Black Hole Event Horizon Schwarzschild Radius (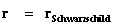 ), with an infinitely “large value”, of any “gravitational field” or “electrostatic field”, isolated and conserved system.
), with an infinitely “large value”, of any “gravitational field” or “electrostatic field”, isolated and conserved system.
The geometry used to describe the space, space-time, or gravitational field surrounding a “Physical Singularity” is Non-Euclidean Spherically Symmetric; and all of Kepler’s Three (3) Laws of gravitational motion are valid.
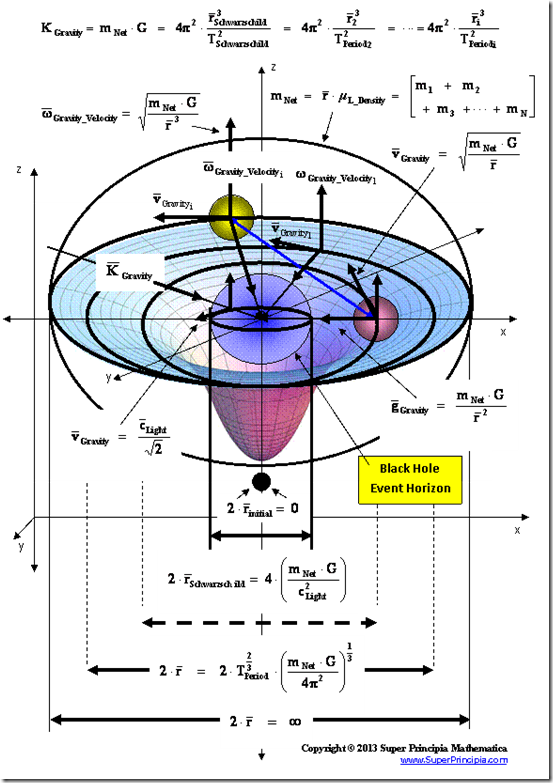
Non-Euclidean – Spherically Symmetric – Schwarzschild Metric
1.2
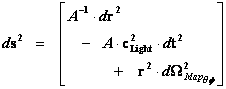 ;
; 
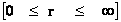 ;
; 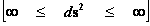
|
Non-Euclidean
Spherically Symmetric
Schwarzschild Metric
(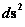 ) )
|
Spherically Symmetric Semi-Major Radius (Distance/Space)
(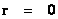 ) )
|
Spherically Symmetric Semi-Major Radius (Distance/Space)
Black Hole Event Horizon
( ) )
|
Spherically Symmetric Semi-Major Radius (Distance/Space)
( ) )
|
|
Schwarzschild Metric (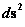 ) )


|

Infinitely Small Value
“Physical”
Singularity
|
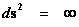
Infinitely Large Value
“Coordinate”
Singularity
|
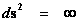
Infinitely Large Value
Infinitely
“Large Area”
|
Physical Singularities (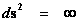 ) with “extreme curvature” can be found in all the Metric Equations, of General Relativity, where there are “Black Hole Event Horizons”, which include: the Schwarzschild metric, the Reissner–Nordström metric, and the Kerr metric, among various other metric equations in the scientific literature; in which all have a “Coordinate Singularity” (
) with “extreme curvature” can be found in all the Metric Equations, of General Relativity, where there are “Black Hole Event Horizons”, which include: the Schwarzschild metric, the Reissner–Nordström metric, and the Kerr metric, among various other metric equations in the scientific literature; in which all have a “Coordinate Singularity” (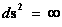 ).
).
Another name for a “Physical Singularity” is a “Naked Singularity”, “Gravitational Singularity”, or “Space-time Singularity” that is enclosed by a “Black Hole Event Horizon”, and is a location at the center of the space-time gravitational field, where there is “extreme curvature”; and the quantities that are used to measure the gravitational field become infinite, in a way that does not depend on the coordinate system.
1.3. Non-Euclidean – Hyperbolically Symmetric – Kruskal-Szekeres Metric and the “Naked Singularity”
In General Relativity, a “Naked Singularity” is manifest in the predictions of the Non-Euclidean Hyperbolically Symmetric “Kruskal-Szekeres” Metric (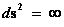 ), whenever there is an input of radius equals to zero (
), whenever there is an input of radius equals to zero (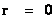 ) into the equation.
) into the equation.
The Non-Euclidean Hyperbolically Symmetric “Kruskal-Szekeres” Metric (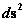 ) is an equation that describes a “geodesic” world “line element” (
) is an equation that describes a “geodesic” world “line element” (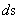 ), as a real curving or warping of physical space, space-time, or a gradient gravitational field, that is hyperbolically symmetric, surrounding a condensed matter, net inertial mass (
), as a real curving or warping of physical space, space-time, or a gradient gravitational field, that is hyperbolically symmetric, surrounding a condensed matter, net inertial mass (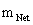 ), or energy source.
), or energy source.
The Kruskal-Szekeres Metric (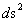 ) is a mathematical equation which describes a “geodesic” world “line element” (
) is a mathematical equation which describes a “geodesic” world “line element” (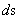 ), of a Riemannian manifold with hyperbolically symmetric curvature of space-time, in the “presence” of matter or the Net (
), of a Riemannian manifold with hyperbolically symmetric curvature of space-time, in the “presence” of matter or the Net (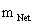 ) Mass, of a localized gradient gravitational field; whose space-time geodesic extends from a “Naked Singularity” at radius equals zero (
) Mass, of a localized gradient gravitational field; whose space-time geodesic extends from a “Naked Singularity” at radius equals zero (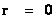 ), then extends into infinite (
), then extends into infinite (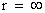 ) distances of that localized space-time gravity field.
) distances of that localized space-time gravity field.
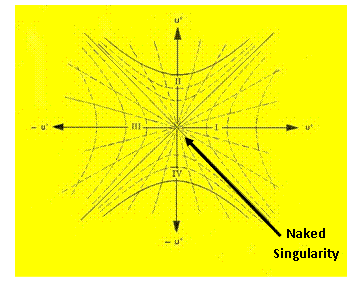
The Kruskal-Szekeres Metric (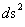 ) predicts “extreme curvature” singularities located at radius equals to zero (
) predicts “extreme curvature” singularities located at radius equals to zero (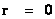 ).
).
For the Kruskal-Szekeres Metric (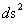 ) there is a “Black Hole” and a “Naked Singularity” (
) there is a “Black Hole” and a “Naked Singularity” (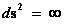 ), with an infinitely “large value”, located at the origin, or center (
), with an infinitely “large value”, located at the origin, or center (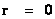 ) for every “Black Hole”, “gravitational field”, or “electrostatic field”, isolated and conserved system.
) for every “Black Hole”, “gravitational field”, or “electrostatic field”, isolated and conserved system.
In General Relativity, a “Naked Singularity” is a “Physical Singularity”, “Gravitational Singularity”, or “Space-time Singularity” that is not enclosed by a “Black Hole Event Horizon”, and is a location at the center of the space-time gravitational field, where there is “extreme curvature”; and the quantities that are used to measure the gravitational field become infinite, in a way that does not depend on the coordinate system”.
The geometry used to describe the space, space-time, or gravitational field surrounding a “Naked Singularity” is a Non-Euclidean Hyperbolic Symmetric Metric.
Non-Euclidean – Hyperbolically Symmetric – Kruskal-Szekeres Metric
1.3

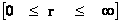 ;
; 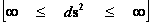
|
Non-Euclidean
Hyperbolically Symmetric
Kruskal-Szekeres Metric
(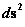 ) )
|
Semi-Major Radius (Distance/Space)
(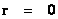 ) )
|
Semi-Major Radius (Distance/Space)
Black Hole Event Horizon
( ) )
|
Semi-Major Radius (Distance/Space)
( ) )
|
|
Kruskal-Szekeres Metric – (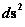 ) )
![clip_image002[17] clip_image002[17]](https://superprincipia.files.wordpress.com/2013/03/clip_image00217_thumb.gif?w=349&h=138)
|
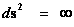
Infinitely Large Value
“Naked”
Singularity
|
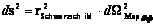
Value
|
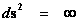
Infinitely Large Value
Infinitely
“Large Area”
|
Naked Singularities with this “extreme curvature” can be found in all the Metric Equations, of General Relativity, where there are no “Black Hole Event Horizons”, which include: Kruskal–Szekeres coordinates, Eddington–Finkelstein coordinates, and Rindler coordinate, among various other metric equations; in which neither have a “Coordinate Singularity”.
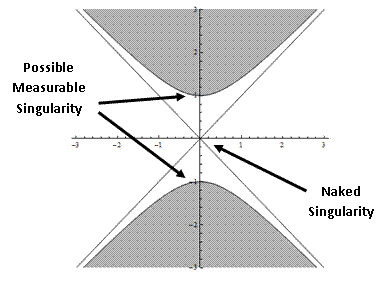
Inside the “Black Hole”, the “Physical Singularity” is completely enclosed by a surface boundary known as the “Event Horizon”; inside the “Black Hole” the density, force, and pressure of the “singularity” is strong enough so that light cannot escape to the outside surface of the Black Hole Event Horizon.
The “Naked Singularity” is completely free from any enclosed surface boundary known as the “Event Horizon”; and similarly there the density, force, and pressure of the “singularity” are strong enough so that light cannot escape “Naked Singularity”.
The theoretical existence of “Physical/Naked Singularities” could be somewhat important, when it comes to measurement, because their existence would mean that it would be possible to observe the collapse of an object, to infinite density at a point; in a space, space-time, or gravitational field.
And at the same time these “extreme curvature” “Physical/Naked Singularities” are not important at all, because they have no observed, impact on mass or charge bodies in motion, relative to other bodies in motion in the universe.
The most commonly discussed concepts of space and time measurements of “black holes”, is that an external observer, outside of the “Event Horizon” cannot observe events taking place in the space-time, within the event horizon. Hence, objects located inside of the “Black Hole Event Horizon”, including the “Physical/Naked Singularity” itself, cannot be directly observed.
If this is true, then this means that General Relativity Theory, when using the Non-Euclidean Spherically Symmetric Metric (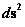 ), equations, cannot make predictions about the future evolution of space-time near “Physical/Naked Singularities” (
), equations, cannot make predictions about the future evolution of space-time near “Physical/Naked Singularities” (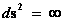 ).
).
Furthermore, if the problem of the Black Hole Event Horizon “Coordinate Singularity”, which manifest in mathematics of the Non-Euclidean “Schwarzschild” Metric (c), is resolved or eliminated, there is no reason to assume that a “Physical/Naked Singularity”, by contrast, is not observable from the outside of a “Black Hole Event Horizon”. The problem still remains of singularities at the center of a matter, net inertial mass (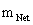 ), or condensed energy gravity source.
), or condensed energy gravity source.
According to modern literature of General Relativity Theory, the “Geodesic Incompleteness Theorem” predicts that the “Black Hole Singularity” is a place that objects, or light rays, can reach in a finite time, and where the curvature becomes extreme, infinite, incomplete, or space-time stops being a Riemann manifold.
Also there are the Penrose–Hawking singularity theorems, which describe a space-time with a singularity, to be a “space-time” that contains “geodesics” that cannot be extended in a smooth manner, past the singularity, which is at the end or start of the geodesic; and this also is called “Geodesic Incompleteness”.
The end or start of such a “Riemann Manifold” is described by the geodesic world line (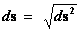 ), and the Penrose–Hawking singularity theorems, is considered to be the “Physical/Naked Singularities” with extreme curvature, and at zero distance (
), and the Penrose–Hawking singularity theorems, is considered to be the “Physical/Naked Singularities” with extreme curvature, and at zero distance (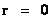 ) of a space-time, as measured relative to a Spherically/Hyperbolically Symmetric center, of a Net Inertial Mass (
) of a space-time, as measured relative to a Spherically/Hyperbolically Symmetric center, of a Net Inertial Mass (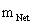 ) gravitational field source, which extends outward into an infinite distance (
) gravitational field source, which extends outward into an infinite distance (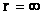 ), relative to that same center.
), relative to that same center.
What causes “Singularities”, are “Singularities” Created?
There is a discussion in the physics community about what causes singularities. Until, now, it was never mentioned, what was the cause of singularities or black holes? This I did to show that it is possible to talk about “Singularities” without describing a cause.
Therefore, the concept of what causes a “Singularity” is a question regarding whether a “Singularity” is a real physical thing, which exist in nature? Or is a “Singularity” just an “infinitesimal limit” or “infinitely large limit” in the resulting output of the mathematics of Non-Euclidean Metric equations, which describe how space, space-time, gravitational field, or electrostatic field behaves, curves, or warps in the presence of condensed matter, mass, or energy.
What causes a “Singularity” some theorize, is created from rotating black holes, in which it is shown that a singularity, spinning rapidly, can become a ring-shaped object.
Likewise, what is the cause of a “Black Hole”, some theorize that the cause of a “Black Hole, is a “Singularity” rotating fast enough that it might be created by the collapse of dust in a Magellan Clouds or Interstellar Nurseries, or by a supernova of a fast-spinning star.
In this respect this is similar to, which came first the “chicken or the egg”, likewise which came first, the “Black Hole or the Singularity”.
Remember, a “Black Hole” is “Physical Singularity” enclosed by a spherical “Event Horizon”. And likewise, a “Black Hole” could also be considered a “Naked Singularity” without an “Event Horizon” enclosure. Whether the Non-Euclidean geometry surrounding a matter source is hyperbolic or spherical symmetric, is the key identifier.
There are also current theories within General Relativity which predict that any star collapsing beyond the Schwarzschild radius ( ) would form a “Black Hole”, inside which a physical singularity, which is covered by an “Event Horizon” would be formed, as all the matter would flow into a physical singularity, point, or a circular line, if the black hole is rotating.
) would form a “Black Hole”, inside which a physical singularity, which is covered by an “Event Horizon” would be formed, as all the matter would flow into a physical singularity, point, or a circular line, if the black hole is rotating.
This collapsing star would result in two event horizons, as well as an “Ergosphere”, which draw closer together as the spin of the singularity increases.
The theory goes on further to say, that when the outer and inner event horizons merge, they shrink toward the rotating singularity, and eventually expose the singularity to the rest of the universe.
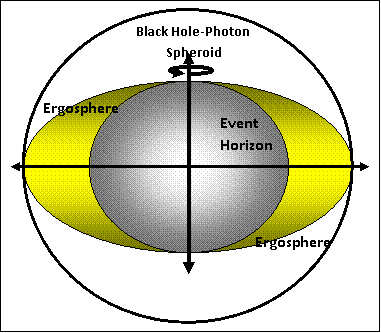
And lastly, there are theories that predict “Singularities” emit light or electromagnetic radiation.
Some, of these new concepts and ideas is what this work attempts to synthesize, in a way that provokes thought, new mathematics, and new physics.
1.4. Big Bang Singularity
According to General Relativity and the “Lambda-Cold-Dark-Matter (ΛCDM)” model, the initial state or origin of the universe, at the beginning of the “Big Bang”, was a “Singularity”.
Mainstream physics believes that both “General Relativity” and “Quantum Mechanics” breaks down when describing the Big Bang as a Singularity.
According to current “Big Bang Theory” discussion, it is not possible to predict what might come “out” of a “Big Bang Singularity” in our past, or what happens to an observer that falls “in” to a “Black Hole Singularity” in the future, so “current physics thinking” assumes that there is a requirement for a modification to some physical law.
They don’t know which law, but they assume that some law must be modified; if there is such a thing as a “Black Hole Singularity”!
In my opinion, there is no agreement with the mainstream physics community, as to whether a “Big Bang Singularity” is a “Black Hole Physical/Naked Singularity” (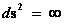 ), or whether it is an “Inverse Distance Power Law Singularities” (
), or whether it is an “Inverse Distance Power Law Singularities” ( ).
).
It is possible, and is described in various modern literature, that the “Big Bang Singularity” is a totally different type of “singularity” from the three (3) described above. One “theory” is that the “Big Bang Singularity” is different because it had to have “spawned” off the other types of “singularities”.
The “Physical Universe” and everything in it, is theorized to originate from the “Big Bang Singularity”, but the term can also refer to the early hot, dense phase, which can be considered the “birth” of our Universe.
How close it can be extrapolated backwards in time towards the “Big Bang Singularity” is most certainly debated. Currently it is predicted that our measuring instruments if at all possible, certainly could get no closer, than the end of the Planck epoch; which includes: Planck Mass, Planck Length, and Planck Time.
Extrapolation of the expansion of the Universe backwards in time using the tools of “General Relativity” and the “Lambda-Cold-Dark-Matter (ΛCDM)” model, yields an infinite density and temperature, at a finite time in the past limited by the “Planck Time” (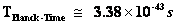 ), of the Planck Epoch.
), of the Planck Epoch.
Any time interval predicted below this “Planck Time” ( ) time Epoch, is considered a “singularity” which signals the breakdown of general relativity; according to popular science.
) time Epoch, is considered a “singularity” which signals the breakdown of general relativity; according to popular science.
|
Big Bang Early Universe Planck Epoch
Equations & Constants
|
|
Planck Mass
(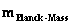 ) )
|
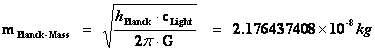
|
|
Planck Length
(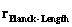 ) )
|

|
|
Planck Time
(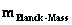 ) )
|
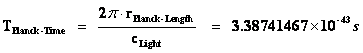
|
The age of the Universe, has a calculated age of “13.7 Billion Years Old”, since its evolution from a “Singularity”, and from the “Planck Epoch” and the “Planck Time” (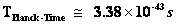 ); since the “Big Bang” event. The Big Bang Theory is based on measurements of the expansion of the universe, using the following tools:
); since the “Big Bang” event. The Big Bang Theory is based on measurements of the expansion of the universe, using the following tools:
· Type Ia supernovae
· Measurements of temperature fluctuations in the cosmic microwave background (CMB)
· Measurements of the correlation function of galaxies
The agreement of these three independent measurements strongly supports the presently accepted “Lambda-Cold-Dark-Matter (ΛCDM)” model that describes in detail the contents of the Universe.
The early phases of the “Big Bang Theory” are subject to much speculation; and rejection. In the most common models the “Early Universe” was filled with matter and radiation that was isotropic and homogeneous, with very high energy density, and with very large temperatures and pressures; and at the very beginning, the universe was very rapidly expanding and cooling.
The current “Big Bang Theory” describes a single originating event, the “Big Bang Singularity”, which was not an explosion, but the abrupt appearance of expanding space-time from this “Singularity”, containing very high electromagnetic heat radiation at temperatures. The “Big Bang Theory” further predicts, that approximately (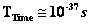 ) seconds into the expansion, a phase transition caused a cosmic inflation, during which the Universe grew exponentially.
) seconds into the expansion, a phase transition caused a cosmic inflation, during which the Universe grew exponentially.
The early universe remained above (10,000 K) for several hundred thousand years, after the “Big Bang”, this is a gaseous state that is detectable as a residual “Cosmic Microwave Background” (CMB); a very low energy radiation emanating from all parts of the sky, in the universe.
The “Big Bang Theory” proposes that a “Big Bang” event, originated from a “Singularity”, along with the concept of “Cosmic Inflation” which happened shortly after the initial bang; and is the only current cosmological model, which is consistent, with the currently observed “expansion of space”, the observed distribution of lighter elements in the universe: (hydrogen, helium, and lithium).
The “Big Bang Theory” also confirms the measured, spatial texture of minute irregularities or anisotropies in the Cosmic Microwave Background (CMB) radiation; which is observed and detected.
Cosmic inflation is also necessary to address what is known as the “horizon problem” in the Cosmic Microwave Background (CMB) of the expanding universe. The current data seems to indicate that the “Expanding Universe” is larger than the “Observable particle or electromagnetic horizon of the universe. This means that the boundaries of the universe will always be bigger, than we can “see” beyond, using “light” electromagnetic radiation as a detecteor!
The accepted “Big Bang Theory” uses the “Lambda-Cold-Dark-Matter (ΛCDM)” model, the “FLRW metric”, the “Friedmann equations”, Hubble’s Law, and the “Cosmological Equations of State” to describe the observable universe, at a time right after the inflationary Planck epoch, to present time, and towards the future. The currently accepted “Big Bang Theory” uses the following Mathematical Models:
· “Lambda-Cold-Dark-Matter (ΛCDM)” model,
· “FLRW metric”,
· “Friedmann equations”,
· “Hubble’s Law”
· “Cosmological Equations of State”
1.5. Cosmic Censorship Hypothesis
The “Cosmic Censorship Hypotheses” is a conceptual prediction and mathematical conjecture regarding whether all of the predictions of General Relativity Theory, are detectable and measurable, and regarding the existence and physical structure of “Singularities” in the universe.
The hypothesis was conceived by Roger Penrose in 1969, and debated by Steven Hawking, Kip Thorne, and others in the following years.
As described earlier “Physical Singularities” arise in the Non-Euclidean Spherically Symmetric Metric (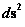 ) solutions of Einstein and Schwarzschild equations, which are typically hidden within “Black Hole Event Horizons”, and located at the radius equal zero (
) solutions of Einstein and Schwarzschild equations, which are typically hidden within “Black Hole Event Horizons”, and located at the radius equal zero (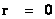 ) centers of the “electrostatic field” or “gravitational field”; and according to assumption, therefore cannot be seen from the rest of space-time.
) centers of the “electrostatic field” or “gravitational field”; and according to assumption, therefore cannot be seen from the rest of space-time.
These “Physical Singularities” with “Black Hole Event Horizons” are described mathematically by Elliptical and Spherical Symmetric Conic Sections.
In general relativity the “Schwarzschild Metric” (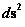 ) equation, is a coordinate system that describes “Spherical/Elliptical Symmetric Symmetry”, surrounding a matter source such that the geometry describes curvature, and in the mathematics there is a “Physical Singularity”, a “Black Hole” with an “Event Horizon” at the center, and located at the radius equal zero (
) equation, is a coordinate system that describes “Spherical/Elliptical Symmetric Symmetry”, surrounding a matter source such that the geometry describes curvature, and in the mathematics there is a “Physical Singularity”, a “Black Hole” with an “Event Horizon” at the center, and located at the radius equal zero (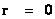 ) centers of the “electrostatic field” or “gravitational field”.
) centers of the “electrostatic field” or “gravitational field”.
The “Schwarzschild Metric” (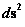 ) equation, further predicts that there is a “Coordinated Singularity”, a “Black Hole” with an “Event Horizon” at the center, and located at the radius equal Schwarzschild Radius (
) equation, further predicts that there is a “Coordinated Singularity”, a “Black Hole” with an “Event Horizon” at the center, and located at the radius equal Schwarzschild Radius (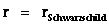 ) of the “gravitational field”.
) of the “gravitational field”.
However, using the proper mathematics this “Coordinated Singularity” can be eliminated from the predictions of the “Schwarzschild Metric” (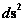 ) equation. And once the “Coordinated Singularity” the “Schwarzschild Metric” equation has been eliminated, it has the advantage, in that it covers the entire space-time manifold, and would be well-behaved everywhere outside the “Physical Singularity”.
) equation. And once the “Coordinated Singularity” the “Schwarzschild Metric” equation has been eliminated, it has the advantage, in that it covers the entire space-time manifold, and would be well-behaved everywhere outside the “Physical Singularity”.
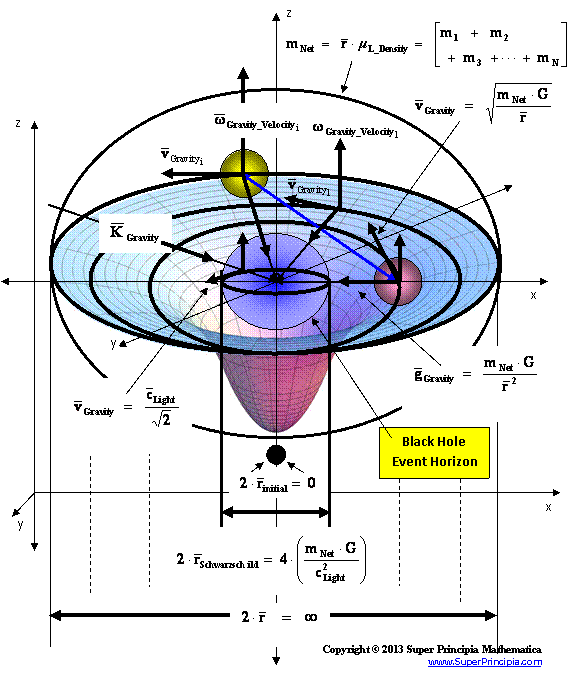
“Singularities” which are not so hidden behind these “Black Hole Event Horizons” are called “Naked Singularities”. These Naked Singularities, are also located at the radius equal zero (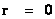 ) centers of the “electrostatic field” or “gravitational field”; and according to assumption, therefore are able to be seen from the rest of space-time.
) centers of the “electrostatic field” or “gravitational field”; and according to assumption, therefore are able to be seen from the rest of space-time.
These “Naked Singularities” without “Black Hole Event Horizons” are described mathematically by Hyperbolic Symmetric Conic Sections.
In General Relativity, the “Kruskal–Szekeres Metric” (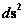 ) equation, is a coordinate system that describes Non-Euclidean “Hyperbolic Symmetric Symmetry”, surrounding a matter source, such that the geometry describes curvature, and in the mathematics there is a “Naked Singularity” (
) equation, is a coordinate system that describes Non-Euclidean “Hyperbolic Symmetric Symmetry”, surrounding a matter source, such that the geometry describes curvature, and in the mathematics there is a “Naked Singularity” (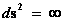 ), which is a “Black Hole” without an “Event Horizon” at the center of a gravity source, and is located at the radius equal zero (
), which is a “Black Hole” without an “Event Horizon” at the center of a gravity source, and is located at the radius equal zero (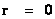 ) centers, of the “electrostatic field” or “gravitational field”.
) centers, of the “electrostatic field” or “gravitational field”.
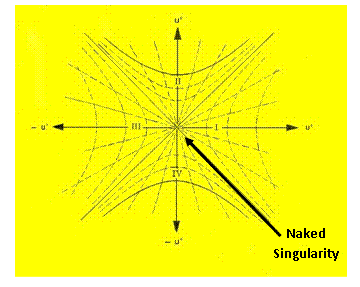
The “Kruskal–Szekeres Metric” ( ) equation, coordinates have the advantage in that they cover the entire space-time manifold, and are well-behaved everywhere outside the “Physical Singularity”.
) equation, coordinates have the advantage in that they cover the entire space-time manifold, and are well-behaved everywhere outside the “Physical Singularity”.
The “Kruskal–Szekeres Metric” (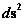 ) equation, and coordinates are also well-behaved even at the Schwarzschild Semi-Major Radius (
) equation, and coordinates are also well-behaved even at the Schwarzschild Semi-Major Radius (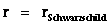 ); where there would normally be a “Coordinate Singularity”.
); where there would normally be a “Coordinate Singularity”.
In essence using “Kruskal–Szekeres Metric” (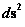 ) equation allows you to eliminate the “Coordinate Singularity” (
) equation allows you to eliminate the “Coordinate Singularity” (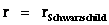 ) of a manifold, but the “Naked Singularity” at the center, where radius equals zero (
) of a manifold, but the “Naked Singularity” at the center, where radius equals zero (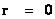 ) remains.
) remains.
Then there are the Penrose–Hawking singularity theorems, which have been generalized to two (2) conjectures, which apply physics to the concept of the nature of “singularities”. They address the singularities which have been found to result during the initial conditions, of the General Relativity Non-Euclidean Metric equations, and likewise there is the “Big Bang Singularity” which denotes the initial condition of the Universe, predicted by Big Bang Theory.
The Penrose–Hawking’s singularity theorem guarantees that some sort of geodesic incompleteness occurs inside any black hole, and that Black Holes are always enclosed by Event Horizons. Nature abhors a Naked Singularity!
The Hawking’s singularity theorem applies to the whole universe, and works backwards-in-time guaranteeing that the “Big Bang” initial event has infinite density. Hawking’s current position, as document in in “A Brief History of Time (1988), (p50)” where he states: “There was in fact no singularity at the beginning of the universe”.
Hawking’s singularity theorem currently predicts that General Relativity Theory must break down at times less than the Planck Epoch of the “Planck Time” (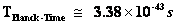 ). Hence general relativity cannot be used to show any singularity. In essence this makes the claims that there are no singularities in nature.
). Hence general relativity cannot be used to show any singularity. In essence this makes the claims that there are no singularities in nature.
The Penrose–Hawking singularity theorems describe two (2) conjectures the “Weak Cosmic Censorship” and the “Strong Cosmic Censorship” hypotheses which are concerned with the global geometry of space, space-times, gravitational, or electrostatic fields.
The Penrose–Hawking singularity theorems use the concept of “Geodesic Incompleteness” which is another name for a geodesic infinite curvature, which extends from (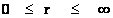 ); and at one end of the infinite “geodesic” curvature there is a Physical Singularity or a Naked Singularity. The Choice between a Physical Singularity and Naked Singularity is a choice between Spherically Symmetric geometry and Hyperbolically Symmetric geometry of a space, space-time, gravitational field, or electrostatic field, surrounding condensed matter.
); and at one end of the infinite “geodesic” curvature there is a Physical Singularity or a Naked Singularity. The Choice between a Physical Singularity and Naked Singularity is a choice between Spherically Symmetric geometry and Hyperbolically Symmetric geometry of a space, space-time, gravitational field, or electrostatic field, surrounding condensed matter.
“Geodesic Incompleteness” is also the concept that there are geodesics, of infinitely curve paths, given by the following limits (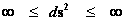 ), which measuring observers traveling along through space-time, can only be extended for a finite time; as the measuring observer traveling along the infinitely curve path must come to an end location, where the observer will encounter a singularity. Presumably, at the end of the infinite curvature geodesic, an within a finite time, the observer will have fallen into a singularity or ends up following some other path, at which the laws of physics are not currently predicted or where General Relativity Theory breaks down.
), which measuring observers traveling along through space-time, can only be extended for a finite time; as the measuring observer traveling along the infinitely curve path must come to an end location, where the observer will encounter a singularity. Presumably, at the end of the infinite curvature geodesic, an within a finite time, the observer will have fallen into a singularity or ends up following some other path, at which the laws of physics are not currently predicted or where General Relativity Theory breaks down.
The Penrose–Hawking–Thorne Weak Cosmic Censorship hypothesis, asserts there can be no “singularity” visible from future null infinity. In other words, “singularities” need to be hidden from an observer at infinity by the event horizon of a black hole. This also means that there are no “Naked Singularities” in nature only “Physical Singularities” shrouded by Black Hole Event Horizons exist in the nature of the universe.
Likewise, this Weak Cosmic Censorship hypothesis also gives a preference for using a Spherically/Ellipsoidal Symmetric Metric, given by the Schwarzschild Metric (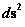 ) equation, and coordinates, as opposed to using a Hyperbolic Symmetric Metric, given by the “Kruskal–Szekeres Metric” (
) equation, and coordinates, as opposed to using a Hyperbolic Symmetric Metric, given by the “Kruskal–Szekeres Metric” (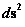 ) equation, and coordinates; which is used as a mathematical tool in General Relativity Theory, for describing how space, space-time, or gravitational field is warped or curved in the presence of a Net Inertial Mass/Matter source.
) equation, and coordinates; which is used as a mathematical tool in General Relativity Theory, for describing how space, space-time, or gravitational field is warped or curved in the presence of a Net Inertial Mass/Matter source.
Aphorism: The Weak Cosmic Censorship claims or conjectures that no “Naked Singularities” can exist in nature, other than the “Big Bang Singularity”. Only “Physical Singularities” exists within Black Hole Event Horizons enclosures; the only exception is the “Big Bang Singularity”.
The Penrose–Hawking–Thorne Strong Cosmic Censorship hypothesis, asserts that, General Relativity Theory, is a completely deterministic theory for all values of radius (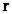 ), in a way similar that classical mechanics is a deterministic theory. In other words, the General Relativity Theory is deterministic, and the fate of all observers should be predictable from all data, including the initial data, where there is zero radius (
), in a way similar that classical mechanics is a deterministic theory. In other words, the General Relativity Theory is deterministic, and the fate of all observers should be predictable from all data, including the initial data, where there is zero radius (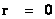 ).
).
Aphorism: The Strong Cosmic Censorship claims or conjectures that that General Relativity “Metric” Theory (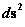 ) is a measurable and deterministic theory, and is predictable from the initial data with zero radius (
) is a measurable and deterministic theory, and is predictable from the initial data with zero radius (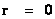 ) and would continue to be predictable with all other radius values, including final data at radius equals to infinity (
) and would continue to be predictable with all other radius values, including final data at radius equals to infinity (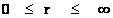 ).
).
The Penrose–Hawking–Thorne two conjectures are mathematically independent, however, one can conceivably come up with contradictory conditions, for which the weak cosmic censorship is valid, but the strong cosmic censorship is violated. Likewise can conceive conditions for which the weak cosmic censorship is violated but the strong cosmic censorship is valid.
1.6. Gravitational Field and Electrostatic Field Inverse Power Laws and Singularities
The “Inverse Distance Power Law” applied to “Gravitational Phenomena” and “Electrostatics Phenomena” predicts that there are various quantities of physics, which diminish as the distance increases, in different powers; such as Gravitational and Electrostatic: Force, Pressure, Linear Density, Volume Density, and Potential Energy.
Inverse Distance Power Law
1.4
( 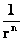 ) ;
) ; 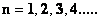
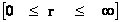 ;
; 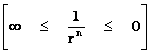
|
Inverse Distance Power Laws
|
|
Three Dimensional
Power Classification
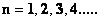
|
Inverse Distance
Power Law
Physical Parameters
( 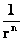 ) )
|
Inverse Space
(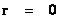 ) )
|
|
Three Dimensional Distance Space
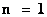
|
( 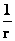 ) )
|
Inverse Distance Space (Inverse Linear or Curvilinear Distance)
|
|
Square of the Distance “Area” Space
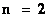
|
( 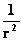 ) )
|
Inverse Square of the Distance Space (Inverse Area)
|
|
Cube Power “Volume” Space
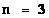
|
( 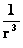 ) )
|
Inverse Cube of the Distance Space (inverse Volume)
|
|
Fourth Power of the Distance Space
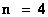
|
( 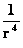 ) )
|
Inverse fourth power of the Distance Space
|
|
Copyright © 2013 Super Principia Mathematica
www.SuperPrincipia.com
|
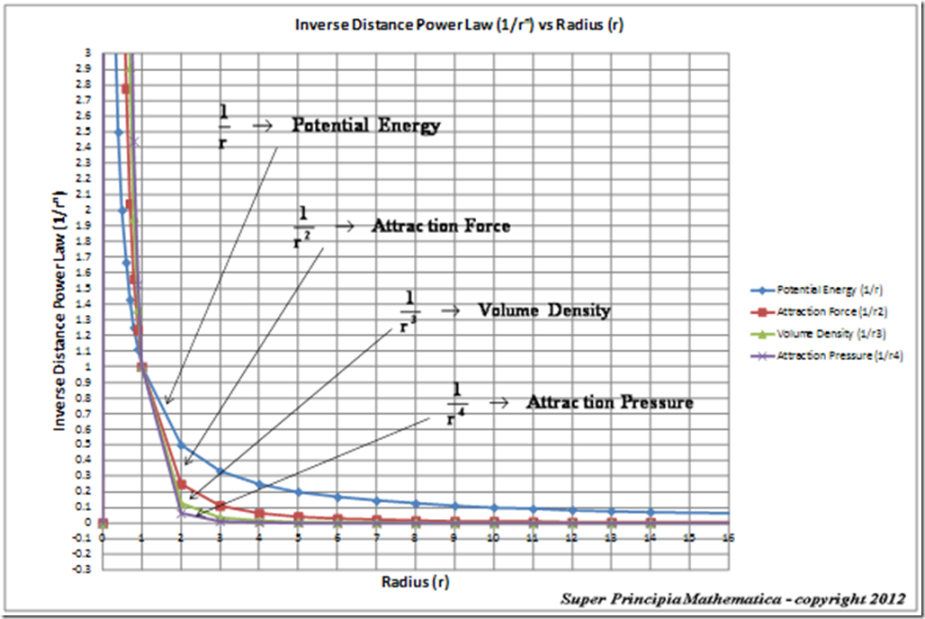
The “Inverse Distance Power Law” applied to each of those various physical parameters in the above table, predicts “Singularities” ( ) at the origin or center and radius equals zero (
) at the origin or center and radius equals zero (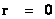 ) of any “gravitational field” or “electrostatic field”, isolated and conserved system.
) of any “gravitational field” or “electrostatic field”, isolated and conserved system.
The “Inverse Distance Power Law Singularity” can be either a “Physical Singularity” enclosed by a Black Hole Event Horizon which is applied to spherically symmetric space-time, or it can be a “Naked Singularity” which is open, and applied to hyperbolic symmetric space-time.
The “Inverse Distance Power Law” likewise predicts “Infinitely Small”, “Zero”, or “Negligible” values at an infinite distance (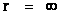 ) away from the center of any “gravitational field” or “electrostatic field” (
) away from the center of any “gravitational field” or “electrostatic field” ( ) isolated and conserved system.
) isolated and conserved system.
I don’t know of any mathematical way, in which to remove or eliminate a singularity from the center of a system, which obeys any form of the Inverse Distance Power Law!
These “Inverse Distance Power Law – Singularities” ( ), are, of course, an example of the mathematical difficulty of divergence to infinite Linear Mass Density, Volume Mass Density, Force, Pressure, and Potential Energy, which reveals a profound problem in our understanding of the physics phenomena, that takes place at the, center (
), are, of course, an example of the mathematical difficulty of divergence to infinite Linear Mass Density, Volume Mass Density, Force, Pressure, and Potential Energy, which reveals a profound problem in our understanding of the physics phenomena, that takes place at the, center (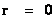 ) of an isolated and conserved system.
) of an isolated and conserved system.
Many in the physics community think that a workable theory of quantum gravity should be able to solve “singularity” problems such as these. I disagree, and believe that “Inverse Distance Power Law – Singularities” ( ) are an artifact of nature that we will always have to deal with!
) are an artifact of nature that we will always have to deal with!
The “Inverse Distance Power Law – Singularities” commonly show up in the physics of the Newtonian Gravitational Force Law (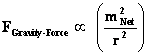 ) and the Gaussian Electrostatics Force Law. (
) and the Gaussian Electrostatics Force Law. (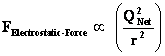 ); whose values depend on the inverse square of the distance “power law”, relative to the origins or center of the gradient “Gravitational Field” or gradient “Electrostatic Field” system body; where (
); whose values depend on the inverse square of the distance “power law”, relative to the origins or center of the gradient “Gravitational Field” or gradient “Electrostatic Field” system body; where (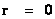 ).
).
And likewise the Inertial Mass Density (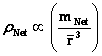 ) and the Electrical Charge Density (
) and the Electrical Charge Density (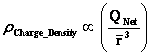 ) of matter, equations among other physical parameters such as: Lineal Density, Pressure, and Potential Energy, all have “Inverse Distance Power Law – Singularities” at the origins or centers (
) of matter, equations among other physical parameters such as: Lineal Density, Pressure, and Potential Energy, all have “Inverse Distance Power Law – Singularities” at the origins or centers ( ) of the gradient “Gravitational Field” or gradient “Electrostatic Field”, of an isolated and conserved system body.
) of the gradient “Gravitational Field” or gradient “Electrostatic Field”, of an isolated and conserved system body.
The following is a list of Inertial Mass Gravitation and Electrostatic parameters that use the “Inverse Distance Power Laws”; and which describe “Singularities” at the origins or centers (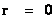 ), and negligible or zero influence at an infinite distance (
), and negligible or zero influence at an infinite distance (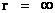 ) away from the origin centers of the “Gravitational Field” or “Electrostatic Field”.
) away from the origin centers of the “Gravitational Field” or “Electrostatic Field”.
Gravitational Field Parameters
|
Inertial Mass Gravitation Parameters
“Bang Singularities”
&
Infinite Distance Observer Interaction
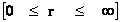 ; ; 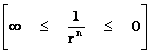
|
|
Various
Inverse Power Law
Physical Parameters
|
Inverse Distance
Power Law
Physical Parameters
(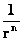 ) )
|
Spherically Symmetric Semi-Major Radius (Distance/Space)
(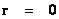 ) )
|
Spherically Symmetric Semi-Major Radius (Distance/Space)
(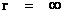 ) )
|
|
Inertial Linear Mass Density
(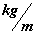 ) )
|
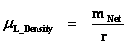
|
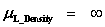
Infinitely Large Value
“Bang Singularity”
|

Zero Value
“Flat Space”
|
|
Self Gravitational Potential Energy
(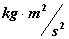 ) )
|

|

Infinitely Large Value
“Bang Singularity”
|

Zero Value
“Flat Space”
|
|
Self Gravitational Force
(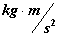 ) )
|
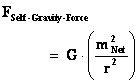
|
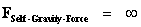
Infinitely Large Value
“Bang Singularity”
|
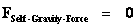
Zero Value
“Flat Space”
|
|
Inertial Volume Mass Density
(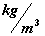 ) )
|

|
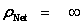
Infinitely Large Value
“Bang Singularity”
|
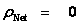
Zero Value
“Flat Space”
|
|
Self Gravitational Pressure
(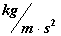 ) )
|
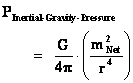
|
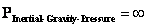
Infinitely Large Value
“Bang Singularity”
|
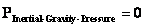
Zero Value
“Flat Space”
|
|
Copyright © 2013 Super Principia Mathematica
www.SuperPrincipia.com
|
Electrostatic Field Parameters
|
Electrostatic Field Parameters
“Bang Singularities”
&
Infinite Distance Observer Interaction
 ; ; 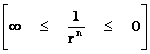
|
|
Various
Inverse Power Law
Physical Parameters
|
Inverse Distance
Power Law
Physical Parameters
(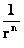 ) )
|
Spherically Symmetric Semi-Major Radius (Distance/Space)
(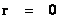 ) )
|
Spherically Symmetric Semi-Major Radius (Distance/Space)
(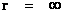 ) )
|
|
Electric Linear Charge Density
( ) )
|
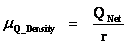
|

Infinitely Large Value
“Bang Singularity”
|
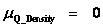
Zero Value
“Flat Space”
|
|
Self Electrostatic Potential Energy
(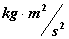 ) )
|
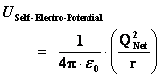
|
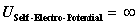
Infinitely Large Value
“Bang Singularity”
|

Zero Value
“Flat Space”
|
|
Self Electrostatic Force
(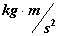 ) )
|

|
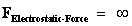
Infinitely Large Value
“Bang Singularity”
|
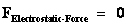
Zero Value
“Flat Space”
|
|
Electric Volume Charge Density
(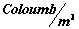 ) )
|

|

Infinitely Large Value
“Bang Singularity”
|

Zero Value
“Flat Space”
|
|
Self Electrostatic Pressure
(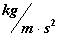 ) )
|
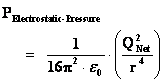
|

Infinitely Large Value
“Bang Singularity”
|

Zero Value
“Flat Space”
|
|
Copyright © 2013 Super Principia Mathematica
www.SuperPrincipia.com
|
1.7. Spherically Symmetric Metric – Limits of Integration – Euclidean & Pseudo-Euclidean Minkowski Metrics
Next, let’s consider the limits of integration for the Spherically SymmetricMetrics (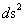 ); Flat Space – Euclidean and Pseudo-Euclidean “Minkowski” “Mass Independent” metrics, where there are no “Singularities” present.
); Flat Space – Euclidean and Pseudo-Euclidean “Minkowski” “Mass Independent” metrics, where there are no “Singularities” present.
Euclidean – Euclidean Metric – Flat Space-Time
1.5
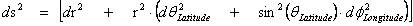 ®
® 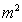
The Euclidean Metric (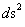 ) radial limits which extend from the center of the gradient gravitational field (
) radial limits which extend from the center of the gradient gravitational field ( ), and into infinite distances (
), and into infinite distances (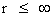 ), is given in this classical form below.
), is given in this classical form below.
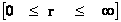 ;
; 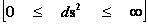
This predicts that the Euclidean Metric (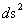 ) is a “Flat Space-Time” and contains or produces no “Singularities” in this form of the metric.
) is a “Flat Space-Time” and contains or produces no “Singularities” in this form of the metric.
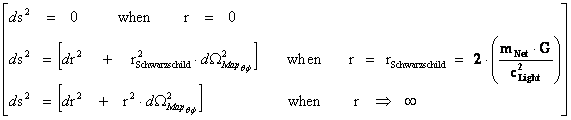

Pseudo-Euclidean – Minkowski Metric – Flat Space-Time
1.6
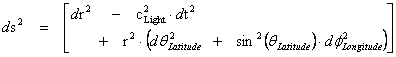 ®
® 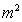
With a metric signature of (-+++) being used. The Minkowski “Flat Space-Time” Metric (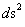 ) has the radial limits which extend from the center of the gravitational field (
) has the radial limits which extend from the center of the gravitational field (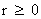 ), and into infinite distances (
), and into infinite distances (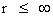 ), is given in this classical form below. (
), is given in this classical form below. ( ). This predicts that the Minkowski Metric (
). This predicts that the Minkowski Metric (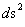 ) contains or produces no “Singularities” in this form of the metric.
) contains or produces no “Singularities” in this form of the metric.
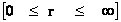 ;
; 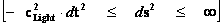
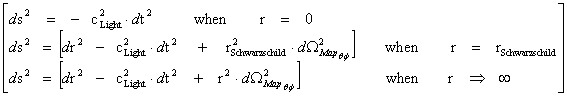

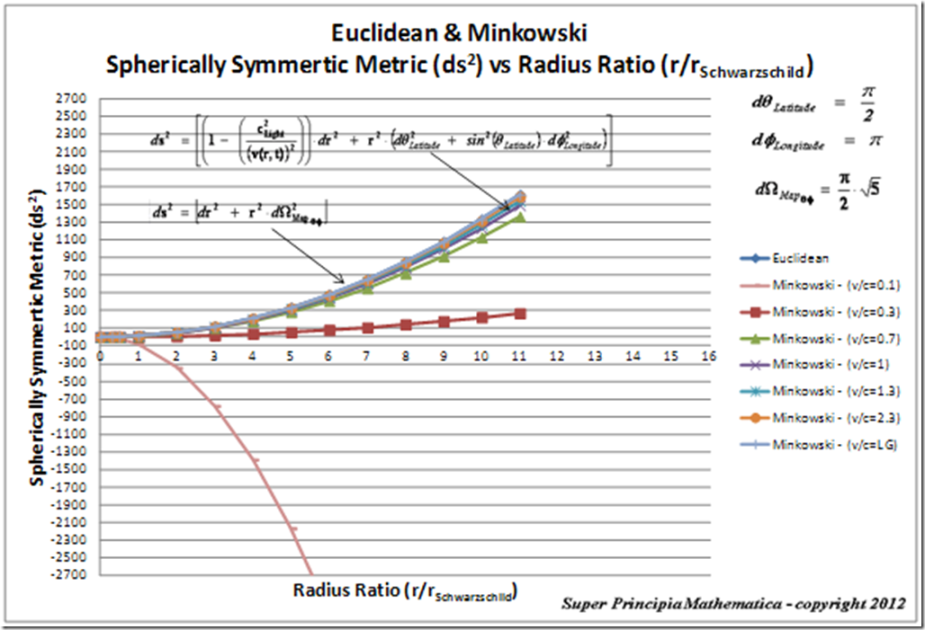
The graph of the Euclidean and Minkowski Metrics (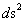 ), predict a “Flat Space-Time”, where the radial integration limits, extend from the center of the gradient gravitational field (
), predict a “Flat Space-Time”, where the radial integration limits, extend from the center of the gradient gravitational field (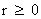 ), and into infinite distances (
), and into infinite distances (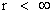 ), away from the center is given in this classical form below.
), away from the center is given in this classical form below.
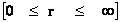 ;
; 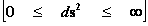
In the graph below the Spherically Symmetric Minkowski Metrics (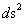 ) are shown at various velocity ratios:
) are shown at various velocity ratios:

And the Surface Curvature components are given by:
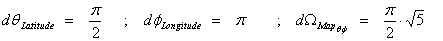
1.8. Spherically Symmetric Metric – Limits of Integration & “Physical” Singularities – Schwarzschild Non-Euclidean Metric
In General Relativity, the Non-Euclidean Spherically SymmetricSchwarzschild “Mass Dependent” Metric (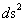 ) describes the geodesic, curving, or warping of a space, space-time, or inhomogeneous gradient gravitational field, in the presence of a net inertial mass/matter (
) describes the geodesic, curving, or warping of a space, space-time, or inhomogeneous gradient gravitational field, in the presence of a net inertial mass/matter (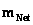 ) source; with a Black Hole Event Horizon, and the “Physical Singularity” at the core source of the isolated and conserved gravitational field.
) source; with a Black Hole Event Horizon, and the “Physical Singularity” at the core source of the isolated and conserved gravitational field.
Spherically Symmetric – Schwarzschild Metric
1.7
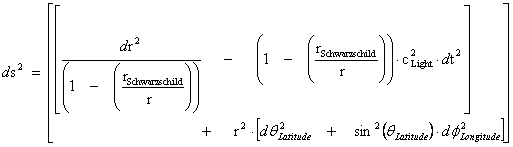 ®
® 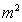
With a metric signature of (-+++) being used. In all of the “modern literature” written on General Relativity, the Schwarzschild Metric (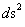 ) yields predictable results “only” in the “exterior region” of the Black Hole Event Horizon source of the gravity field. The predictable results start with any radius relative to center of the gradient gravitational field that is greater than the Schwarzschild Radius (
) yields predictable results “only” in the “exterior region” of the Black Hole Event Horizon source of the gravity field. The predictable results start with any radius relative to center of the gradient gravitational field that is greater than the Schwarzschild Radius (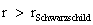 ), and into infinite distances (
), and into infinite distances (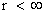 ), of the gradient field.
), of the gradient field.
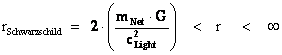
The Exterior solution corresponds to the space outside of the Black Hole Event Horizon, and Schwarzschild Semi-Major Radius ( ).
).
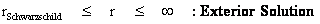
The Interior solution corresponds to the space within or inside the Black Hole Event Horizon, and Schwarzschild Semi-Major Radius ( ).
).
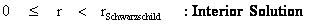
The “modern literature” written on General Relativity, describes that the Schwarzschild Metric (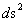 ) predicts that a “Black Hole” has “two (2) Singularities” in the metric of a localized inhomogeneous gravitational field:
) predicts that a “Black Hole” has “two (2) Singularities” in the metric of a localized inhomogeneous gravitational field:
There is one “Physical Singularity” that is an infinitely “small” number located at zero radius (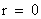 ) of the gradient gravitational field. (
) of the gradient gravitational field. (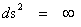 ).
).
And a second “Coordinate Singularity” that is an infinitely “large” number located at the Black Hole Event Horizon, Schwarzschild (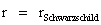 ) Radius of the inhomogeneous gradient gravitational field. (
) Radius of the inhomogeneous gradient gravitational field. (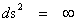 ).
).
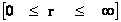 ;
; 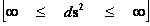
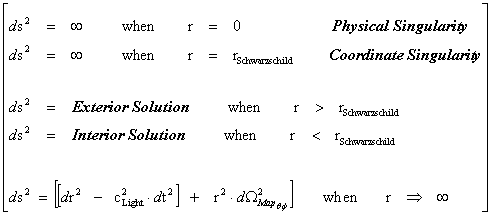

The Schwarzschild Metric (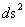 ) predicts the “Physical Singularity” located at zero radius, is “extreme curvature” as the geodesic approaches an infinitely small value, (
) predicts the “Physical Singularity” located at zero radius, is “extreme curvature” as the geodesic approaches an infinitely small value, (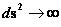 ), as the radius approaches zero (
), as the radius approaches zero (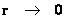 ). The “Physical Singularity” is a natural artifact for any Non-Euclidean metric.
). The “Physical Singularity” is a natural artifact for any Non-Euclidean metric.
The “Coordinate Singularity” is an anomaly, and is an infinitely large value, (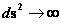 ), with “extreme curvature” of the geodesic as the radius approaches Schwarzschild Radius (
), with “extreme curvature” of the geodesic as the radius approaches Schwarzschild Radius (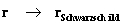 ). This value is an anomaly, and is not a natural artifact for any Non-Euclidean metric.
). This value is an anomaly, and is not a natural artifact for any Non-Euclidean metric.
Furthermore,the Schwarzschild Metric (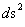 ) predicts, that as the distance relative to a spherically symmetric center, approaches infinity or an infinite distance (
) predicts, that as the distance relative to a spherically symmetric center, approaches infinity or an infinite distance (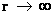 ) away from the “physical singularity”, center, where there is maximum or extreme curvature, the Non-Euclidean“Curved Space-time” becomes Minkowski “Flat Space-time”. This is also known as Non-Euclidean “Geodesic Incompleteness”; of a diverging gravity field.
) away from the “physical singularity”, center, where there is maximum or extreme curvature, the Non-Euclidean“Curved Space-time” becomes Minkowski “Flat Space-time”. This is also known as Non-Euclidean “Geodesic Incompleteness”; of a diverging gravity field.
Pseudo-Euclidean – Minkowski Metric
1.8
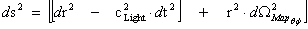 ®
® 
|
Non-Euclidean Spherically Symmetric “Schwarzschild” Metric
“Geodesic Incompleteness” of a Diverging Gravitational Field
Singularities and Infinitely Large Spaces Listed
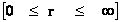 ; ; 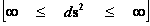
|
|
Non Euclidean “Schwarzschild” Metric
(Curved Space-time)
(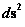 ) )
|
Spherically Symmetric Metric
(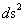 ) )
Spherically Symmetric Semi-Major Radius (Distance/Space)
(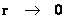 ) )
&
(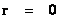 ) )
|
Spherically Symmetric Metric
(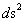 ) )
Spherically Symmetric Semi-Major Radius (Distance/Space)
(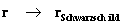 ) )
&
(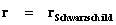 ) )
|
Spherically Symmetric Metric
(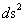 ) )
Spherically Symmetric
Semi-Major Radius (Distance/Space)
(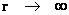 ) )
&
(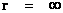 ) )
|
|
Schwarzschild Metric
(Curved Space-time)
(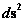 ) )
|
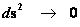
|

|

|
|
Schwarzschild Metric
(Curved Space-time)
(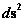 ) )
|
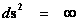
(Infinitely Small)
|
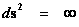
(Infinitely Large)
|
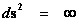
(Infinitely Large)
|
|
Schwarzschild Metric
(Curved Space-time)
(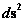 ) )
|
Physical
Singularity
|
Coordinate
Singularity
|
Infinitely Large
Spherically Symmetric
Space-time
|
|
Copyright © 2013 Super Principia Mathematica
www.SuperPrincipia.com
|
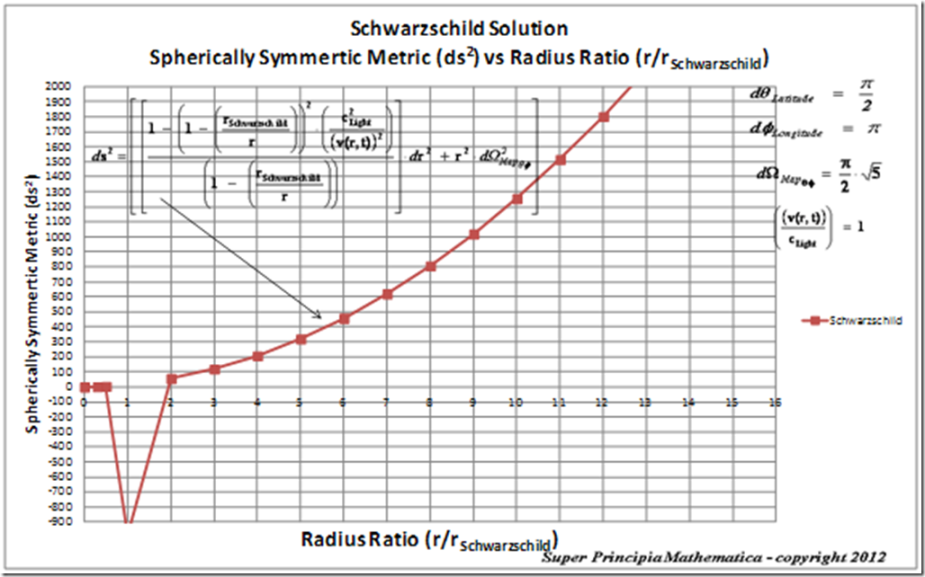
Below is a plot of the Schwarzschild Metric (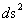 )
)
(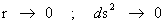 ) Then (
) Then (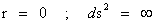 )
)
And 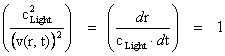
1.9. Hyperbolic Symmetric Metric – Limits of Integration & “Naked” Singularities – Kruskal-Szekeres Non-Euclidean Metric
In General Relativity, the Hyperbolic SymmetricKruskal-Szekeres “Mass Dependent” Metric (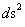 ) describes the curving or warping of a space, space-time, or gravitational field, in the presence of a net inertial mass (
) describes the curving or warping of a space, space-time, or gravitational field, in the presence of a net inertial mass (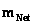 ) source, without a Black Hole Event Horizon enclosure. Next, let’s consider the limits of integration and the “Naked Singularity” of the Kruskal-Szekeres Metric equation.
) source, without a Black Hole Event Horizon enclosure. Next, let’s consider the limits of integration and the “Naked Singularity” of the Kruskal-Szekeres Metric equation.
The Kruskal-Szekeres metric equation and coordinates are sometimes chosen because, they are able to cover the entire extended Schwarzschild manifold, without the problem of a “Coordinate Singularity” and a Black Hole Event Horizon; it has the drawback of involving implicit functions like (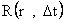 ), and being a much harder calculation.
), and being a much harder calculation.
Due to the complexity of the Kruskal-Szekeres coordinates it makes them difficult to use for actual calculations that require knowledge of the detailed geometry, as opposed to the causal structure.
The Kruskal-Szekeres coordinates were invented only as a solution to resolving the “Coordinate Singularity” located at the Black Hole Event Horizon Surface (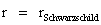 ), of the Schwarzschild coordinates.
), of the Schwarzschild coordinates.
The Kruskal-Szekeres coordinates solution to the “Coordinate Singularity” problem, was to remove the Black Hole Event Horizon, thereby exposing to any measuring observer, a “Naked Singularity.”
The author does not think that the Hyperbolically Symmetric Kruskal-Szekeres Metric (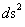 ) equation is a mathematically precise, physical description of nature. The author favors the Spherically SymmetricSchwarzschild Metric (
) equation is a mathematically precise, physical description of nature. The author favors the Spherically SymmetricSchwarzschild Metric (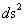 ), and believes that equation, is a more mathematically precise, physical description of nature.
), and believes that equation, is a more mathematically precise, physical description of nature.
However, let’s briefly look at the concepts and mathematics of the Hyperbolically Symmetric Kruskal-Szekeres Metric (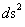 ).
).
The “Hyperbolic Curvature” term (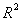 ) is found in the Hyperbolically Symmetric Kruskal-Szekeres Metric (
) is found in the Hyperbolically Symmetric Kruskal-Szekeres Metric (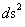 ) and is a square of the distance, or area parameter, that measures the surrounding curving of space, space-time, gravitational field, in the presence of a mass (
) and is a square of the distance, or area parameter, that measures the surrounding curving of space, space-time, gravitational field, in the presence of a mass (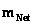 ) body source.
) body source.
Hyperbolically Symmetric Kruskal-Szekeres Metric ─ Hyperbolic Curvature Term (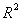 )
)
1.9
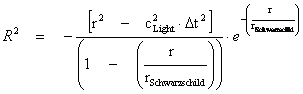 ®
® 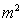
The hyperbolic curvature term ( ) in the Kruskal-Szekeres Metricrepresents differential “Space-Time” (
) in the Kruskal-Szekeres Metricrepresents differential “Space-Time” (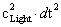 ), and differential “Distance/Space” (
), and differential “Distance/Space” (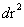 ), in a hyperbolically symmetric space, space-time, or gravitational field as described mathematically in the following:
), in a hyperbolically symmetric space, space-time, or gravitational field as described mathematically in the following:
1.10
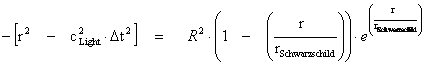 ®
® 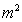
Where the Schwarzschild Radius (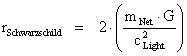 ) is given.
) is given.
The Kruskal-Szekeres coordinates and Metric is given by the following:
Hyperbolically Symmetric Kruskal-Szekeres Metric─ (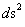 )
)
1.11

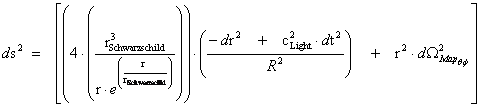
After making substitution, and rearranging, the Kruskal-Szekeres coordinates and Metric is also given by the following:
1.12
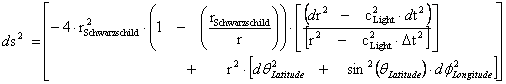 ®
® 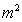
Next letting the space and time term in the equation above equals to the following.
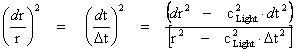
The following mathematical formalism of the Hyperbolically Symmetric Kruskal-Szekeres Metric(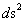 ), I have not seen published in the literature, and is a much more simpler way of understanding the physics, behind the calculation of the metric.
), I have not seen published in the literature, and is a much more simpler way of understanding the physics, behind the calculation of the metric.
“New” Hyperbolically Symmetric Kruskal-Szekeres Metric─ (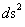 )
)
1.13
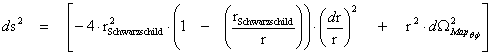 ®
® 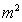
With a metric signature of (-+++) being used. In all of the “modern literature” written on General Relativity, the Kruskal-Szekeres Metric (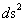 ) claims to yields predictable results in all “hyperbolic” regions away from and surrounding a “Naked Singularity”, where there is extreme curvature at the center of a net inertial mass (
) claims to yields predictable results in all “hyperbolic” regions away from and surrounding a “Naked Singularity”, where there is extreme curvature at the center of a net inertial mass (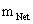 ) body, space, space-time, or gradient gravitational field.
) body, space, space-time, or gradient gravitational field.
Likewise, General Relativity, describes that the Kruskal-Szekeres Metric (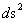 ) predicts one “Naked Singularity” in the origin and center (
) predicts one “Naked Singularity” in the origin and center (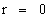 ) of any localized curved space, space-time, or gravitational field, surrounding a Net Inertial Mass/matter (
) of any localized curved space, space-time, or gravitational field, surrounding a Net Inertial Mass/matter (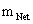 ) source.
) source.
The “Naked Singularity” is an infinitely “Large” number located at zero radius (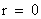 ) of the space, space-time, or gradient gravitational field, described by the Kruskal-Szekeres Metric (
) of the space, space-time, or gradient gravitational field, described by the Kruskal-Szekeres Metric (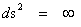 ).
).
The extreme “hyperbolically” curved space, space-time, or gradient gravitational field, described by the hyperbolic geometry of the Kruskal-Szekeres Metric (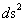 ), and has limits described by the “Geodesic Incompleteness” (
), and has limits described by the “Geodesic Incompleteness” (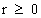 ), and into infinite distances (
), and into infinite distances (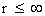 ), away from the “Naked Singularity” is given below.
), away from the “Naked Singularity” is given below.
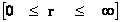 ;
; 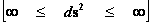
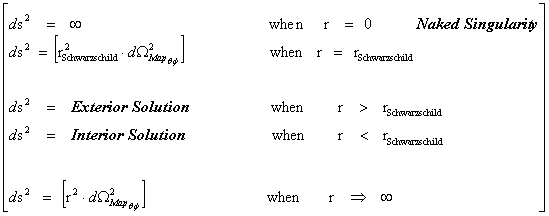
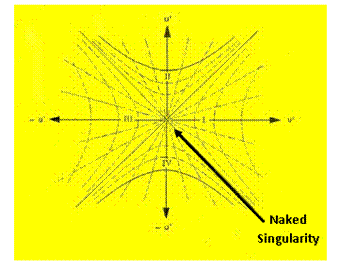
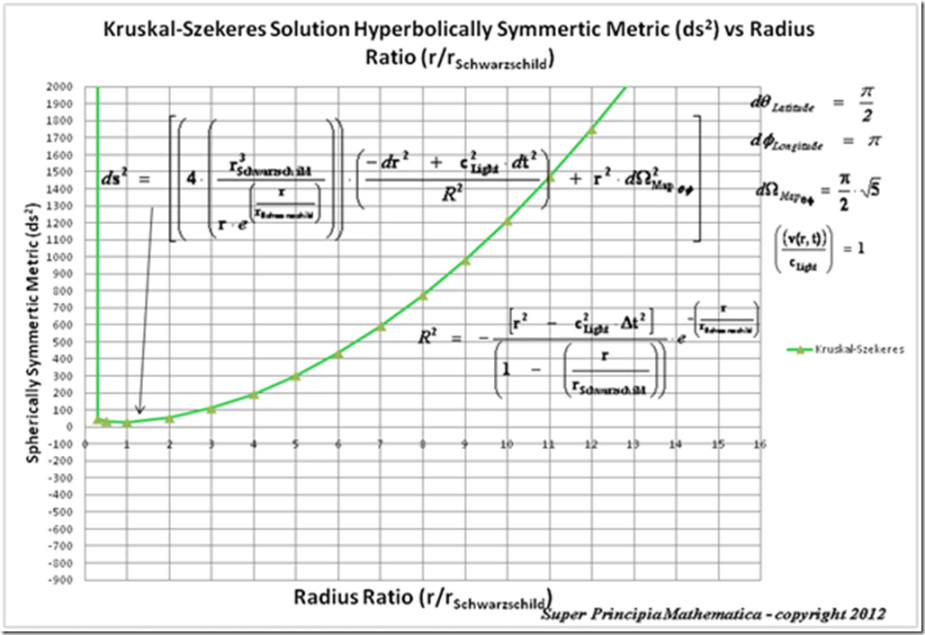
The Kruskal-Szekeres Metric (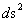 ) predicts a “Naked Singularity” located at zero radius, is a value that approaches an infinitely large value, as the radius approaches zero.
) predicts a “Naked Singularity” located at zero radius, is a value that approaches an infinitely large value, as the radius approaches zero.
The “Naked Singularity” (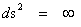 ) requires accepting that there are no Black Holes with Event Horizons in nature. The author predicts that “Naked Singularities” do not exist!
) requires accepting that there are no Black Holes with Event Horizons in nature. The author predicts that “Naked Singularities” do not exist!
Furthermore,the Kruskal-Szekeres Metric (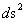 ) predicts, that as the distance relative to a hyperbolically symmetric center approaches infinite distance(
) predicts, that as the distance relative to a hyperbolically symmetric center approaches infinite distance(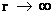 ) or an infinite distance away from the “Naked singularity” and maximum curvature, the Non-Euclidean“Curved Space-time” becomes “Flat Space” independent of Time. This is also known as the “Geodesic Incompleteness”.
) or an infinite distance away from the “Naked singularity” and maximum curvature, the Non-Euclidean“Curved Space-time” becomes “Flat Space” independent of Time. This is also known as the “Geodesic Incompleteness”.
2-Sphere Manifold Surface Area Metric
1.14
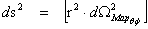 ®
® 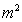
|
Non-Euclidean Hyperbolically Symmetric “Kruskal-Szekeres”
“Mass Dependent” Metric
Singularities and Infinitely Large Spaces
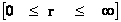 ; ; 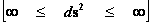
|
|
Non Euclidean “Kruskal-Szekeres” Metric
(Curved Space-time)
(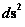 ) )
|
Hyperbolically Symmetric Metric
(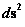 ) )
Hyperbolically Symmetric Semi-Major Radius (Distance/Space)
(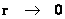 ) )
&
(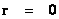 ) )
|
Hyperbolically Symmetric Metric
(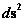 ) )
Hyperbolically Symmetric Semi-Major Radius (Distance/Space)
(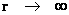 ) )
&
(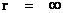 ) )
|
|
Kruskal-Szekeres Metric
(Curved Space-time)
(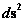 ) )
|
|

|
|
Kruskal-Szekeres Metric
(Curved Space-time)
(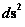 ) )
|
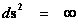
(Infinitely Large)
|
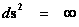
(Infinitely Large)
|
|
Kruskal-Szekeres Metric
(Curved Space-time)
(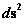 ) )
|
Naked
Singularity
|
Infinitely Large
Spherically Symmetric
Space-time
|
|
Copyright © 2013 Super Principia Mathematica
www.SuperPrincipia.com
|
Below is a plot of the Kruskal-Szekeres Metric (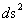 )
)
( ) Then (
) Then (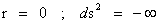 )
)
And 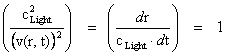
1.10. Geodesic Incompleteness
The Penrose–Hawking singularity theorems use the concept of “Geodesic Incompleteness” which is another name for a geodesic with infinite curvature, which extends from (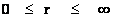 ); and at one end of the infinite “geodesic” curvature, with a metric output (
); and at one end of the infinite “geodesic” curvature, with a metric output ( ), there is a Physical Singularity or a Naked Singularity, and at the opposite spectrum infinite space, or area.
), there is a Physical Singularity or a Naked Singularity, and at the opposite spectrum infinite space, or area.
The Choice between a Physical Singularity and Naked Singularity is a choice between Spherically Symmetric geometry and Hyperbolically Symmetric geometry, and whether there is a “Black Hole Event Horizon” in a space, space-time, gravitational field, or electrostatic field surrounding a mass or charge source.
Remember that a Physical Singularity is an “Infinitely Small Number” predicted by the Schwarzschild Spherically Symmetric Metric (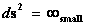 ); located at the center of a gravitational field, or electrostatic field.
); located at the center of a gravitational field, or electrostatic field.
And the Naked Singularity is an “Infinitely Large Number” predicted by the Kruskal-Szekeres Hyperbolically Symmetric (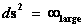 ) Metric; located at the center of a gravitational field, or electrostatic field.
) Metric; located at the center of a gravitational field, or electrostatic field.
“Geodesic Incompleteness” is also the concept that there are geodesics, of infinitely curve paths, which measuring observers traveling along through space-time, can only be extended for a finite time; as the measuring observer traveling along the infinitely curve path must come to an end location, where the observer will encounter a singularity, and where the mathematics are undefined:
· “Geodesic Incompleteness” limits of integration ─ (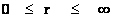 )
)
· Euclidean Metric ─ (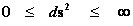 )
)
· Minkowski Metric ─ (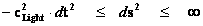 )
)
· Schwarzschild Metric ─ (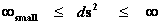 )
)
· Kruskal-Szekeres ─ (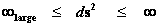 )
)
Therefore, at the end of the “Non-Euclidean” infinite curvature geodesics, an within a finite time, the observer will have fallen into a singularity, or ends up following some other path, at which the laws of physics are not currently predicted, undefined, or where General Relativity Theory breaks down.
|
Geodesic Incompleteness
Euclidean, Minkowski, Schwarzschild, and Kruskal-Szekeres Space-Time Metrics
|
|
Metric Type
|
Spherically & Hyperbolically Symmetric Metric
(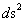 ) )
Semi-Major Radius (Distance/Space)
(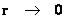 ) )
|
Spherically & Hyperbolically Symmetric Metric
(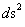 ) )
Semi-Major Radius
(Distance/Space)
(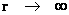 ) )
|
|
Euclidean Metric
(Flat Space)
(Mass Independent)
|
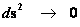
|
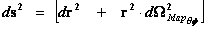
|
|
Pseudo Euclidean “Minkowski” Metric
(Flat Space-time)
(Mass Independent)
|
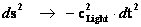
|

|
|
Non Euclidean “Schwarzschild” Metric
(Curved Space-time)
(Mass Dependent)
|
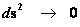
|

|
|
As the distance relative to a spherically symmetric center approaches zero (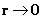 ) )
“Curved Space-time” becomes
Infinitesimally Small Space
(Physical Singularity)
|
As the distance relative to a spherically symmetric center approaches infinity (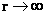 ) )
Non-Euclidean
“Curved Space-time” becomes
Minkowski
“Flat Space-time”
|
|
Non Euclidean “Kruskal-Szekeres” Metric
(Curved Space-time)
(Mass Dependent)
|
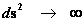
|
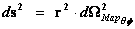
|
|
As the distance relative to a spherically symmetric center approaches zero (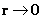 ) )
“Curved Space-time” becomes
Infinitely Large Space
(Naked Singularity)
|
As the distance relative to a spherically symmetric center approaches infinity (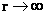 ) )
Non-Euclidean
“Curved Space-time” becomes
“Flat Space-time”
|
|
Copyright © 2013 Super Principia Mathematica
www.SuperPrincipia.com
|
The “Geodesic Incompleteness” table describes Euclidean, Minkowski, Schwarzschild, and Kruskal-Szekeres Metrics above, shows that only the Minkowski Metric does not end “Zero” or “Incompleteness”. The Minkowski Metric predicts (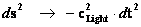 ).
).
All singularities are not the same!
The Euclidean Metric (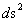 ), Minkowski Metric (
), Minkowski Metric (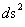 ), Kruskal-Szekeres Metric (
), Kruskal-Szekeres Metric (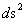 ), & Schwarzschild Metric (
), & Schwarzschild Metric (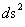 )
)
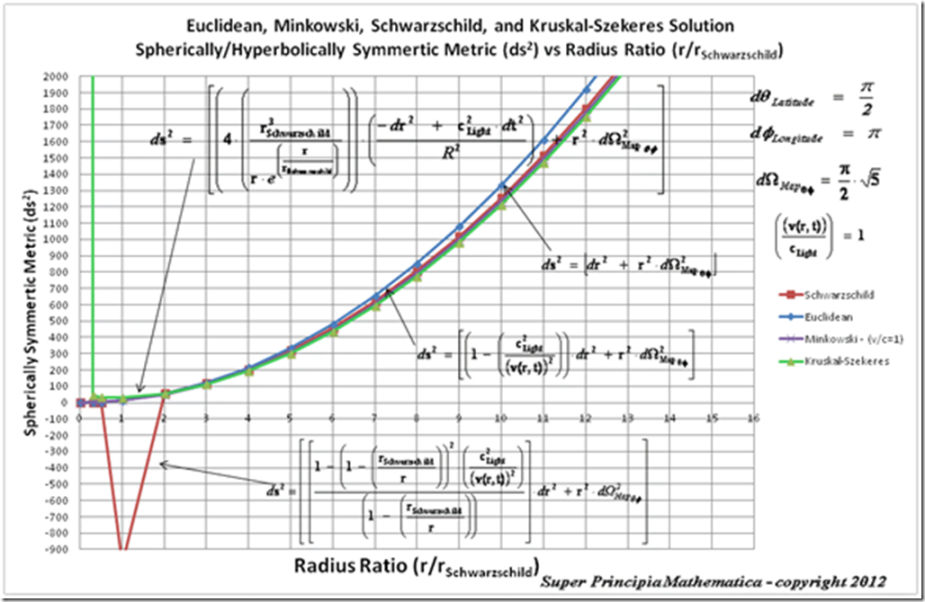
The “Geodesic Incompleteness” table along with the “Metric Equations” of the Euclidean, Minkowski, Schwarzschild, and Kruskal-Szekeres Metrics below, shows that only the Minkowski Metric does not end in “Zero” or “Incompleteness”. (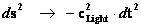 ).
).
|
Geodesic Incompleteness
Euclidean, Minkowski, Schwarzschild, and Kruskal-Szekeres Gravitational & Space-Time Metrics
|
|
Metric Classification
|
Spherically & Hyperbolically Symmetric Metric
(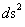 ) )
|
Semi-Major Radius (Distance/Space)
(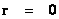 ) )
|
Semi-Major Radius (Distance/Space)
(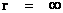 ) )
|
|
Euclidean Metric
Mass Independent
|
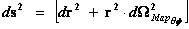
|
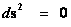
Zero Value
Empty Space
“Point Particle”
|
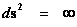
Infinitely Large Value “Space”
“Flat Space”
|
|
Pseudo Euclidean “Minkowski” Metric
Mass
Independent
|

|
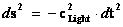
Non-Zero Negative Value “Time-Like”
“Space-Time”
|
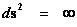
Infinitely Large Value “Space”
“Flat Space”
|
|
Non Euclidean
“Schwarzschild”
Metric
Mass
Dependent
|


|
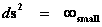
Infinitely Small Value “Space”
“Physical Singularity”
|
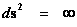
Infinitely Large Value “Space”
“Flat Space”
|
|
Non Euclidean
“Kruskal-Szekeres”
Metric
Mass
Dependent
|
![clip_image002[6] clip_image002[6]](https://superprincipia.files.wordpress.com/2013/03/clip_image0026_thumb.gif?w=363&h=142)
|
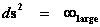
Infinitely Large Value “Space”
“Naked Singularity”
|
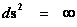
Infinitely Large Value “Space”
“Flat Space”
|
|
Copyright © 2013 Super Principia Mathematica
www.SuperPrincipia.com
|
1.11. Geodesic Completeness, Null Geodesics, & Space-Time Manifolds
The concept of “Geodesic Completeness” which is another name for a “Gaussian/Riemann Manifold” or “Surface” which is described by a “Null Geodesic” of finite curvature, which extends from (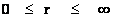 ), when the Spherically/Hyperbolically Symmetric Metric is equal to zero (
), when the Spherically/Hyperbolically Symmetric Metric is equal to zero (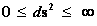 ).
).
In general two adjacent “local” points, of a geodesic, on a manifold resembles Euclidean space, although globally a manifold could be Non-Euclidean. For example, the surface of the sphere is not a Euclidean space, but in a local region or area on the sphere, it can be charted on geographic maps into a flat Euclidean plane.
One important class of geodesics on manifolds is the class of differentiable manifolds that is “Covariant” between inertial and non-inertial frames of reference; that is denoted by the equation (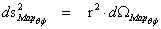 ); and because calculus can be done on manifolds and their surface area.
); and because calculus can be done on manifolds and their surface area.
A differentiable manifold can be described using mathematical maps, called coordinate charts, collected in a mathematical form that proves that a frame of reference on a Gaussian/Riemann manifold/surface, has a defined set of coordinates, which can have a zero, Black Hole “Naked Singularity” or a “Physical Singularity” at the center of that coordinate system.
A general Riemannian metric on a four (4) dimensional manifold allows for Non-Euclidean distances, and longitude ( ) and latitude (
) and latitude (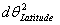 ) angles, to be measured; likewise “Covariant” “geodesic arc-length” (
) angles, to be measured; likewise “Covariant” “geodesic arc-length” (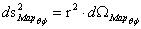 ) exists between inertial and non-inertial frames of reference.
) exists between inertial and non-inertial frames of reference.
Gaussian/Riemann Manifold – Map/Patch/Manifold Surface Metric
1.15
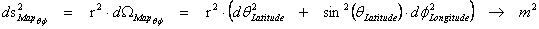
Geodesic motion is an idealization of a path described by a Metric, where one assumes the existence of test mass particles which all follow geodesic from point to point, through a space, space-time or gravitational field, in which they reside. “Geodesic completeness” at one end of the Gaussian/Riemann 2-Sphere, Manifold/Surface is a finite “Null geodesic” Non-Euclidean curvature, there is a Physical Singularity or a Naked Singularity, and this manifold is extended into an infinite distance away from any zero or singularity source.
“Geodesic completeness” (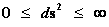 ) is also the concept that when the Spherically/Hyperbolically Symmetric Metric is equal to zero (
) is also the concept that when the Spherically/Hyperbolically Symmetric Metric is equal to zero ( ), there is a Gaussian/Riemann Manifold/Surface that describe geodesics, with finitely curve paths, which measuring observers traveling along through space-time, can be extended for an infinite time. As the measuring observer traveling along the infinitely curve path could never come to an end location, where the observer will encounter a singularity.
), there is a Gaussian/Riemann Manifold/Surface that describe geodesics, with finitely curve paths, which measuring observers traveling along through space-time, can be extended for an infinite time. As the measuring observer traveling along the infinitely curve path could never come to an end location, where the observer will encounter a singularity.
The “Null Geodesic Completeness” (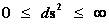 ) predicts when the Spherically/Hyperbolically Symmetric Metric is equal to zero (
) predicts when the Spherically/Hyperbolically Symmetric Metric is equal to zero ( ), the differential “Space” and “Time” are predicted along the geodesics of a manifold which is either Euclidean or Non-Euclidean, and its coordinates are equal to a negative of the Map/Patch/Manifold Surface Metric (
), the differential “Space” and “Time” are predicted along the geodesics of a manifold which is either Euclidean or Non-Euclidean, and its coordinates are equal to a negative of the Map/Patch/Manifold Surface Metric (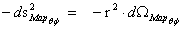 ).
).
Null Geodesic Completeness Theorem ( )
)
1.16
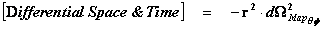
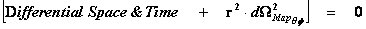
Because of this feature described above of “Null Geodesics” ( ), it is said that only “mass-less” electromagnetic particle-waves with a rest mass of zero, like the photon, will follow null geodesics:
), it is said that only “mass-less” electromagnetic particle-waves with a rest mass of zero, like the photon, will follow null geodesics:
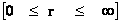 ;
; 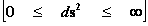
· “Geodesic Completeness” Null Geodesic Condition ─ ( )
)
· Euclidean Metric ─ (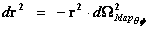 )
)
· Minkowski Metric ─ (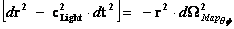 )
)
· Schwarzschild Metric ─ (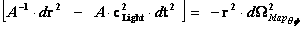 )
)
· Kruskal-Szekeres ─ ( )
)
|
Geodesic Completeness, Null Geodesic & Space-Time Manifolds
Euclidean, Minkowski, Schwarzschild, and Kruskal-Szekeres Metrics
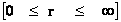 ; ; 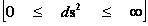
|
|
Metric Classification
|
Spherically & Hyperbolically Symmetric Metric “Manifolds”
(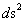 ) )
|
2-Sphere Manifolds
(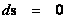 ) )
|
|
Euclidean Metric
Mass Independent
|
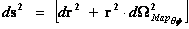
|
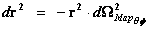
|
|
Pseudo Euclidean “Minkowski” Metric
Mass
Independent
|
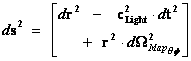
|
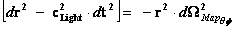
Non-Zero Negative Value “Time-Like”
“Space-Time”
|
|
Non Euclidean
“Schwarzschild”
Metric
Mass
Dependent
|


|

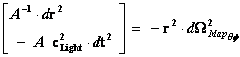
Infinitely Small Value “Space”
“Physical Singularity”
|
|
Non Euclidean
“Kruskal-Szekeres”
Metric
Mass
Dependent
|
![clip_image002[21] clip_image002[21]](https://superprincipia.files.wordpress.com/2013/03/clip_image00221_thumb.gif?w=343&h=138)
|
![clip_image002[23] clip_image002[23]](https://superprincipia.files.wordpress.com/2013/03/clip_image00223_thumb.gif?w=355&h=102)
Infinitely Large Value “Space”
“Naked Singularity”
|
|
Copyright © 2013 Super Principia Mathematica
www.SuperPrincipia.com
|
1.12. Non-Euclidean Metrics & Inverse Distance Power Law Conundrum
There is a Conundrum in physics regarding all “Singularities”. The physics and the mathematics predict that there are “Physical Singularities” or “Naked Singularities” and “Inverse Distance Power Law Singularities” in the physical same location.
What does this mean for physics and measurement?
This allows us to describe hypotheses which will also be described later; and is stated by the following aphorisms below:
Aphorism: The Cosmic “Conundrum” Censorship claims or conjectures that “Inverse Distance Power Law Singularities” describe infinitely large values ( ), and the “Physical Singularities” (
), and the “Physical Singularities” ( ) describe infinitely small values, and the “Naked Singularities” (
) describe infinitely small values, and the “Naked Singularities” ( ) describe infinitely large values, of space, space-time, gravitational field, or the electrostatic field, in the same location of zero radius (
) describe infinitely large values, of space, space-time, gravitational field, or the electrostatic field, in the same location of zero radius (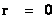 ); what are the implications? Is the singularity measurable?
); what are the implications? Is the singularity measurable?
Aphorism: The Strong Cosmic Censorship claims or conjectures that that General Relativity “Metric” Theory (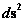 ) is a measurable and deterministic theory (
) is a measurable and deterministic theory (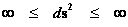 ), and is predictable from all data, including the initial data with zero radius (
), and is predictable from all data, including the initial data with zero radius (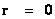 ) and would continue to be predictable with all other radius values, including final data at infinite radius (
) and would continue to be predictable with all other radius values, including final data at infinite radius (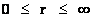 ).
).
Aphorism: The Strong Cosmic “Most Probable” Censorship claims or conjectures that that General Relativity “Metric” Theory (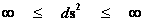 ) is a completely measurable and deterministic theory, only within a certain range, and is not predictable from the initial data, with zero radius (
) is a completely measurable and deterministic theory, only within a certain range, and is not predictable from the initial data, with zero radius (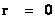 ), and the final data, where radius equals to infinity (
), and the final data, where radius equals to infinity (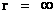 ), and would only be predictable and deterministic, with all other radius values, between the initial and final input values (
), and would only be predictable and deterministic, with all other radius values, between the initial and final input values (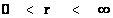 ).
).
The above General Relativity aphorisms apply to the Non-Euclidean Spherically/Hyperbolically Symmetric Metric (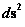 ) equations, and the Inverse Distance Power Law ((
) equations, and the Inverse Distance Power Law (( 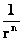 ) ;
) ; 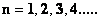 ) equations, predict values on both “Cosmological” and “Quantum Mechanical” scales; and is conceptualized below.
) equations, predict values on both “Cosmological” and “Quantum Mechanical” scales; and is conceptualized below.
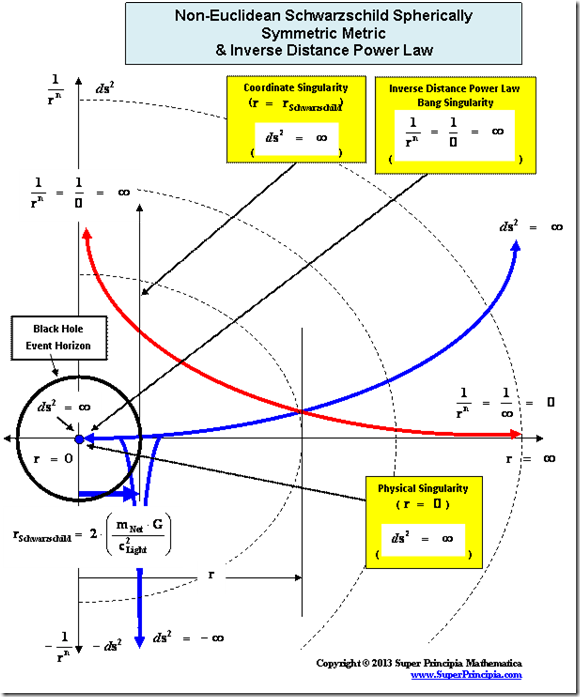
|
Non-Euclidean Schwarzschild Spherically Symmetric Metric
& Inverse Distance Power Law
Incompleteness Positions/Locations
|
|
Semi-Major Radius (Distance/Space)
|
Inverse Distance
Power Law
Physical Parameters
(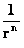 ) )
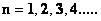
|
Non-Euclidean Schwarzschild Spherically Symmetric Metric


|
|
Semi-Major Radius (Distance/Space)
(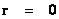 ) )
|
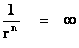
Infinitely Large Value
“Bang Singularity”
|
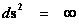
Infinitely Small Value
“Curved Space-time”
“Physical Singularity”
|
|
Semi-Major Radius (Distance/Space)
(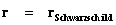 ) )
|
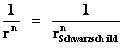
Finite Value
“Black Hole”
“Event Horizon”
|
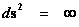
Infinitely Large Value
“Curved Space-time”
“Coordinate Singularity”
|
|
Semi-Major Radius (Distance/Space)
(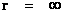 ) )
|
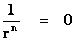
Zero Value
“Flat Space”
|
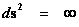
Infinitely Large Value
“Flat Space-time”
|
|
Copyright © 2013 Super Principia Mathematica
www.SuperPrincipia.com
|
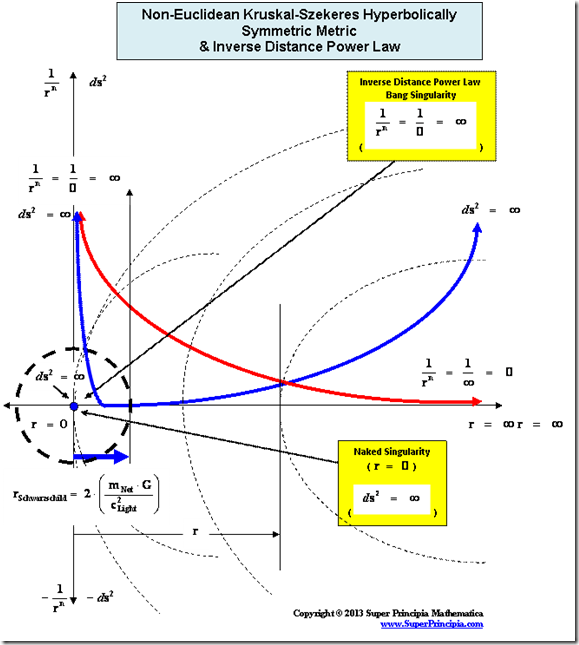
|
Non-Euclidean Kruskal-Szekeres Hyperbolically Symmetric Metric
& Inverse Distance Power Law
Incompleteness Positions/Locations
|
|
Semi-Major Radius (Distance/Space)
|
Inverse Distance
Power Law
Physical Parameters
(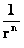 ) )
|
Non-Euclidean Kruskal-Szekeres Hyperbolically Symmetric Metric
![clip_image002[25] clip_image002[25]](https://superprincipia.files.wordpress.com/2013/03/clip_image00225_thumb.gif?w=323&h=131)
|
|
Semi-Major Radius (Distance/Space)
(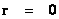 ) )
|
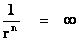
Infinitely Large Value
“Bang Singularity”
|
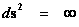
Infinitely Small Value
“Curved Space-time”
“Physical Singularity”
|
|
Semi-Major Radius (Distance/Space)
(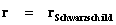 ) )
|
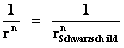
Finite Value
“Black Hole”
“Event Horizon”
|

Infinitely Large Value
“Curved Space-time”
“Coordinate Singularity”
|
|
Semi-Major Radius (Distance/Space)
(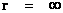 ) )
|
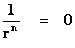
Zero Value
“Flat Space”
|
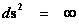
Infinitely Large Value
“Flat Space-time”
|
|
Copyright © 2013 Super Principia Mathematica
www.SuperPrincipia.com
|
1.13. Extended Cosmic Censorship Hypotheses
The following is an attempt by the author at conceptualizing, postulating, and extending the Cosmic Censorship hypotheses, so that the contradictions of the Penrose–Hawking–Thorne two Weak and Strong Cosmic Conjectures could be eliminated; and that all singularity theorem conditions, could be accounted for.
These newly added “Cosmic Censorships” also extends the Special Relativity postulates of Einstein.
The Cosmic Censorship hypothesis was first formulated by Roger Penrose in 1969, and it has yet to be stated in a completely mathematical or conceptually formalized way; like the approach described in this work.
This work is aimed at a more formal statement, that is mathematically and physically reasonable, and that can be proved to be true or false; and likewise is described in such a way that the “Cosmic Censorships” are generally interesting.
The following aphorisms are meant to extend the Weak and the Strong Cosmic Censorship hypotheses, and Einstein’s Special Relativity postulates:
Aphorism 1.1: The Cosmic Censorship claims or conjectures that all singularities: “Physical, Naked, and Inverse Distance Power Law Singularities” are manifested on Cosmological and Quantum Mechanical scales; including the “Big Bang Singularity”.
Aphorism 1.2: The Cosmic Completeness Censorship claims or conjectures that there are no Null geodesics of a manifold of infinite extension, which end in “Singularities”, in Euclidean and Minkowski, “Flat Space” Metric geometry; where geodesics end in Null geodesics, or smooth space-time manifolds (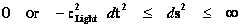 ). The Null geodesics of a manifold of infinite extension described by Non-Euclidean Spherically/Hyperbolically Symmetric Metric geometry ends incomplete, in “Physical or Naked Black Hole Singularities” (
). The Null geodesics of a manifold of infinite extension described by Non-Euclidean Spherically/Hyperbolically Symmetric Metric geometry ends incomplete, in “Physical or Naked Black Hole Singularities” (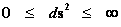 ). Null Geodesics of infinite extension are completely “Covariant” for all observers.
). Null Geodesics of infinite extension are completely “Covariant” for all observers.
Aphorism 1.3: The Cosmic Incompleteness Censorship claims or conjectures that all geodesics of infinite extension, including manifolds, are described by Non-Euclidean Spherically/Hyperbolically Symmetric Metric geometry, which ends incomplete (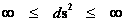 ), in “Physical or Naked Black Hole Singularities”. Geodesics of infinite extension are incompletely “Covariant” for all observers.
), in “Physical or Naked Black Hole Singularities”. Geodesics of infinite extension are incompletely “Covariant” for all observers.
Aphorism 1.4: The Cosmic “Naked” Censorship claims or conjectures that only “Inverse Distance Power Law Singularities” and “Naked Singularities” exist in the universe; including the “Big Bang Singularity”. “Naked Singularities” are open to the universe, and do not have any Black Hole Event Horizons enclosing them.
Aphorism 1.5: The Cosmic “Black Hole” Censorship claims or conjectures that only “Inverse Distance Power Law Singularities” and “Physical Singularities” exist in the universe; including the “Big Bang Singularity”. “Physical Singularities” exists within spherical Black Hole Event Horizons enclosures.
Aphorism 1.6: The Weak Cosmic Censorship claims or conjectures that no “Naked Singularities” can exist in nature, other than the “Big Bang Singularity”. Only “Physical Singularities” exists within Black Hole Event Horizons enclosures; the only exception is the “Big Bang Singularity”.
Aphorism 1.7: The Cosmic “Conundrum” Censorship claims or conjectures that “Inverse Distance Power Law Singularities” describe infinitely large values ( ), and the “Physical Singularities” (
), and the “Physical Singularities” (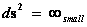 ) describe infinitely small values, and the “Naked Singularities” (
) describe infinitely small values, and the “Naked Singularities” (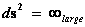 ) describe infinitely large values, of space, space-time, gravitational field, or the electrostatic field, in the same location of zero radius (
) describe infinitely large values, of space, space-time, gravitational field, or the electrostatic field, in the same location of zero radius (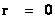 ); what are the implications? Is the singularity measurable?
); what are the implications? Is the singularity measurable?
Aphorism 1.8: The Strong Cosmic Censorship claims or conjectures that that General Relativity “Metric” Theory (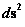 ) is a measurable and deterministic theory (
) is a measurable and deterministic theory (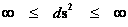 ), and is predictable from all data, including the initial data with zero radius (
), and is predictable from all data, including the initial data with zero radius (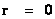 ) and would continue to be predictable with all other radius values, including final data at infinite radius (
) and would continue to be predictable with all other radius values, including final data at infinite radius (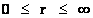 ).
).
Aphorism 1.9: The Strong Cosmic “Most Probable” Censorship claims or conjectures that that General Relativity “Metric” Theory (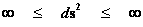 ) is a completely measurable and deterministic theory, only within a certain range, and is not predictable from the initial data, with zero radius (
) is a completely measurable and deterministic theory, only within a certain range, and is not predictable from the initial data, with zero radius (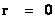 ), and the final data, where radius equals to infinity (
), and the final data, where radius equals to infinity (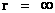 ), and would only be predictable and deterministic, with all other radius values, between the initial and final input values (
), and would only be predictable and deterministic, with all other radius values, between the initial and final input values (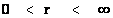 ).
).
Aphorism 1.10: The Strong “Coordinate Singularity” Censorship claims or conjectures that the “Coordinate Singularity” located at the Schwarzschild Radius ( ) is a mathematical anomaly, and can be eliminated with proper mathematical resolution; thereby making the General Relativity “Schwarzschild Metric” Theory (
) is a mathematical anomaly, and can be eliminated with proper mathematical resolution; thereby making the General Relativity “Schwarzschild Metric” Theory (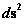 ) measurable, and predictable, at the Black Hole Event Horizon.
) measurable, and predictable, at the Black Hole Event Horizon.
Aphorism 1.11: The Cosmic “Particle Creation” Censorship claims or conjectures that Physical, Naked, and Inverse Power Law Singularities, except for the Big Bang Singularity, can be created around condensing matter, or static charge; and likewise, can be annihilated in the form of heat radiation electromagnetic energy, back into the surrounding universe; therefore all singularities are present where there is rest mass.
Aphorism 1.12: The Cosmic “Photon Energy” Censorship claims or conjectures that propagating “Photons” of electromagnetic energy void of rest mass, have “Singularities” along every point of its wavelength; therefore, Propagating Photons do not have singularities of any kind.
Aphorism 1.13: The Cosmic “Universal Constants” Censorship claims or conjectures that independent of linear, curvilinear, or rotational motion of any frame of reference, all the “Universal Constants” (i.e. Speed of Light Constant ( ), Universal Gravitational Constant (
), Universal Gravitational Constant ( ), Planck’s Quantum of Action (
), Planck’s Quantum of Action ( ) Constants, etc., are “Frame of Reference Invariant”, and remain the same everywhere in the universe, and in all frames of reference; and universal constants do not change over time, and have been the same, since the initial conditions at the very beginning of the Universe.
) Constants, etc., are “Frame of Reference Invariant”, and remain the same everywhere in the universe, and in all frames of reference; and universal constants do not change over time, and have been the same, since the initial conditions at the very beginning of the Universe.
Aphorism 1.14: The Cosmic “Universal Physical Law” Censorship claims or conjectures that independent of linear, curvilinear, or rotational motion, or any location in the universe, all the “Universal Laws of Physics”, remain the same everywhere in the universe, and in all frames of reference.
Aphorism 1.15: The Cosmic “Big Bang” Censorship claims or conjectures that the Universe has an origin, birth, or beginning initial state, known as the “Big Bang”, whose evolution and current state, can be described by predictable physics.
Aphorism 1.16: The Cosmic “Immortal Existence” Censorship claims or conjectures that the Universe is Immortal, has always been, has always existed, and there is no “Big Bang”, origin of the universe, only current evolution and current state, can be described by predictable physics.
2. Conclusion
This work, described five (5) different types or classifications of “Singularities” in nature: the Inverse Distance Power Law Singularity, the Physical Singularity, the Naked Singularity, the Coordinate Singularity, and the Big Bang Singularity. Correlating the nature of these singularities, with the mathematics, and with the real physical world is a conundrum in physics.
This work extends the “Strong and Weak Cosmic Censorship” hypotheses originally proposed by Roger Penrose, Steven Hawking, and Kip Thorne, by adding additional “Censorships” which removes some of the contradiction that exists with just the two (2) original “Weak and Strong Cosmic Censorship Hypotheses” alone.
The Cosmic Censorship hypothesis was first formulated by Roger Penrose in 1969, and it has yet to be stated in a completely mathematical or conceptually formalized way; like the approach described in this work.
The current state of the discussion of the “Cosmic Censorship” in the physics community is to approach the censorships more like a research program thesis or proposal. This work aimed at more formal statements of the “Cosmic Censorship Conjectures” which is mathematically and physically reasonable, can be proved to be true or false, and be interesting to discuss for many years.
The extension of the “Cosmic Censorships” also extends Einstein’s Special Relativity postulates, and opens the door for a real discussion about Black Holes, Singularities, Big Bangs, and the nature of matter.
This work addressed the difference between a Black Hole “Physical Singularity” which is described mathematically by a Non-Euclidean Spherically Symmetric “Schwarzschild” Metric equation, and the Black Hole “Naked Singularity”, described mathematically by the Non-Euclidean Hyperbolically Symmetric “Kruskal-Szekeres” Metric equation.
The author believes that space, space-time, and the gravitational field surrounding condensed matter, is spherical/elliptically symmetric, and is better described by the Schwarzschild Metric, with a mathematical correction for the Coordinate Singularity; and does not believe that space is naturally hyperbolically symmetric surrounding condensed matter, as described by the Kruskal-Szekeres Metric.
This work, addressed the concept of “Geodesic Incompleteness” and “Geodesic Completeness”.
It was demonstrated in this work that the “Geodesic Incompleteness” conjectures, that Geodesics of infinite extension are incompletely “Covariant” for all observers. The “Geodesic Incompleteness”, is another name for a geodesic with infinite curvature, which at one end of the geodesic is a singularity.
The “Cosmic Incompleteness Censorship” likewise, claims or conjectures that all geodesics of infinite extension, including manifolds, are described by Non-Euclidean Spherically/Hyperbolically Symmetric Metric geometry, which ends incomplete (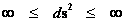 ), in “Physical or Naked Black Hole Singularities”.
), in “Physical or Naked Black Hole Singularities”.
Further, it was demonstrated that the “Geodesic Completeness” conjectures, that Null Geodesics of infinite extension are completely “Covariant” for all observers. The “Geodesic Completeness” also predicts that the Metric geometry for the Null geodesics of a manifold of infinite extension, are given by the range (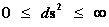 ). Except for the Minkowski Metric which ends, not complete in zero, ends complete in a smooth manifold metric, given by the range (
). Except for the Minkowski Metric which ends, not complete in zero, ends complete in a smooth manifold metric, given by the range (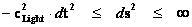 ).
).
This work revealed that there is a conundrum in physics regarding all “Singularities”. The physics and the mathematics predict that there are “Physical Singularities” or “Naked Singularities” and “Inverse Distance Power Law Singularities” in the physical same location.
And the author raises the question mathematically, about different types of singularities in the same location, without giving an answer, for what this means for physics and measurement of singularities?
The author leaves a question remaining, after reading this work; what type of singularity is the “Big Bang Singularity”? Is the Big Bang Singularity similar to aforementioned classification of singularities, or is it different from the “Physical Singularities”, “Naked Singularities”, or “Inverse Distance Power Law Singularities”?
The following statements conceptually summarize some of the discussion in this work:
· At the origin-center (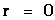 ) of any mass or charged body, there exist Physical Singularity that is infinitely small, and at the same location there exists an Inverse Distance Power Law Singularity that is infinitely large.
) of any mass or charged body, there exist Physical Singularity that is infinitely small, and at the same location there exists an Inverse Distance Power Law Singularity that is infinitely large.
· At the infinite distance (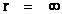 ) away from the center of any mass or charged body, there exist Non-Euclidean Metric that is infinitely large, and at the same location there exists an Inverse Distance Power Law that is infinitely small, zero, or negligible.
) away from the center of any mass or charged body, there exist Non-Euclidean Metric that is infinitely large, and at the same location there exists an Inverse Distance Power Law that is infinitely small, zero, or negligible.
· A Physical Singularity is enclosed by a Black Hole Event Horizon Surface or Volume; and is described by Spherical and Elliptical Conic sections and symmetry.
· A Naked Singularity does not have a Black Hole Event Horizon Surface or Volume enclosing the singularity, and is open; and is described by Hyperbolic Conic sections and symmetry.
· A Coordinate Singularity is an anomaly, and is located at the Black Hole Event Horizon Surface or Volume enclosing a secondary “Physical singularity” at the center of the Black Hole; and is not necessary, and can be eliminated from the mathematics of the Non-Euclidean Spherically Symmetric Metrics.
· The Big Bang Singularity is not fully explained and could be a “Physical Singularity” or a “Naked Singularity” or neither!
· A Physical/Naked Singularity at the center of a “Gravitational” or “Electromagnetic” field system body, has no impact whatsoever, on any mass or charged body being at rest, being in uniform motion, being accelerated, or from interacting with equal and opposite forces with other mass or charge, in the physical universe.
3. Appendix – 1 ─ Original Bet on Naked Singularities: Stephen W. Hawking, John P. Preskill, Kip S. Thorne
In 1991, John Preskill and Kip Thorne bet against Stephen Hawking that nature would never produce a Naked Singularity.
Source: http://www.theory.caltech.edu/people/preskill/old_naked_bet.html
Whereas Stephen W. Hawking firmly believes that naked singularities are an anathema and should be prohibited by the laws of classical physics,
And whereas John Preskill and Kip Thorne regard naked singularities as quantum gravitational objects that might exist unclothed by horizons, for all the Universe to see,
Therefore Hawking offers and Preskill/Thorne accept, a wager with odds of 100 pounds sterling to 50 pounds sterling, that
“When any form of classical matter or field that is incapable of becoming singular in flat spacetime is coupled to general relativity via the classical Einstein equations, the result can never be a naked singularity.”
The loser will reward the winner with clothing to cover the winner’s nakedness. The clothing is to be embroidered with a suitable concessionary message.
Stephen W. Hawking, John P. Preskill, Kip S. Thorne
Pasadena, California, 24 September 1991
Conceded on a technicality by Stephen W. Hawking, 5 February 1997
4. Appendix – 2 ─ New Bet on Naked Singularities: Stephen W. Hawking, John P. Preskill, Kip S. Thorne
In 1997 Hawking conceded the bet, which he characterized as “technicalities”. Hawking later reformulated the bet to exclude those technicalities. The revised bet is still open.
Source: http://www.theory.caltech.edu/people/preskill/new_naked_bet.html
Whereas Stephen W. Hawking (having lost a previous bet on this subject by not demanding genericity) still firmly believes that naked singularities are an anathema and should be prohibited by the laws of classical physics,
And whereas John Preskill and Kip Thorne (having won the previous bet) still regard naked singularities as quantum gravitational objects that might exist, unclothed by horizons, for all the Universe to see,
Therefore Hawking offers, and Preskill/Thorne accept, a wager that
“When any form of classical matter or field that is incapable of becoming singular in flat spacetime is coupled to general relativity via the classical Einstein equations, then A dynamical evolution from generic initial conditions (i.e., from an open set of initial data) can never produce a naked singularity
(a past-incomplete null geodesic from scri-plus).”
The loser will reward the winner with clothing to cover the winner’s nakedness. The clothing is to be embroidered with a suitable, truly concessionary message.
Stephen W. Hawking, John P. Preskill, Kip S. Thorne
Pasadena, California, 5 February 1997
5. Appendix – 3 ─ Table of Cosmic Censorship Hypotheses and the Author’s Viewpoint
Table of Cosmic Censorship Hypotheses, and the author’s viewpoint
|
Aphorisms
|
Cosmic Censorship Hypotheses
|
Kemp’s
Viewpoint
|
|
Aphorism 1.1
Cosmic Censorship
|
The Cosmic Censorship claims or conjectures that all singularities: “Physical, Naked, and Inverse Distance Power Law Singularities” are manifested on Cosmological and Quantum Mechanical scales; including the “Big Bang Singularity”.
|
Yes. I agree
|
|
Aphorism 1.2
Cosmic Completeness Censorship
|
The Cosmic Completeness Censorship claims or conjectures that there are no Null geodesics of a manifold of infinite extension, which end in “Singularities”, in Euclidean and Minkowski, “Flat Space” Metric geometry; where geodesics end in Null geodesics, or smooth space-time manifolds (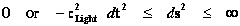 ). The Null geodesics of a manifold of infinite extension described by Non-Euclidean Spherically/Hyperbolically Symmetric Metric geometry ends incomplete, in “Physical or Naked Black Hole Singularities” ( ). The Null geodesics of a manifold of infinite extension described by Non-Euclidean Spherically/Hyperbolically Symmetric Metric geometry ends incomplete, in “Physical or Naked Black Hole Singularities” (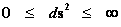 ). Null Geodesics of infinite extension are completely “Covariant” for all observers. ). Null Geodesics of infinite extension are completely “Covariant” for all observers.
|
Yes. I agree
|
|
Aphorism 1.3
Cosmic Incompleteness Censorship
|
The Cosmic Incompleteness Censorship claims or conjectures that all geodesics of infinite extension, including manifolds, are described by Non-Euclidean Spherically/Hyperbolically Symmetric Metric geometry, which ends incomplete (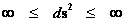 ), in “Physical or Naked Black Hole Singularities”. Geodesics of infinite extension are incompletely “Covariant” for all observers. ), in “Physical or Naked Black Hole Singularities”. Geodesics of infinite extension are incompletely “Covariant” for all observers.
|
Yes. I agree
|
|
Aphorism 1.4
Cosmic “Naked” Censorship
|
The Cosmic “Naked” Censorship claims or conjectures that only “Inverse Distance Power Law Singularities” and “Naked Singularities” exist in the universe; including the “Big Bang Singularity”. “Naked Singularities” are open to the universe, and do not have any Black Hole Event Horizons enclosing them.
|
No. I disagree
|
|
Aphorism 1.5
Cosmic “Black Hole” Censorship
|
The Cosmic “Black Hole” Censorship claims or conjectures that only “Inverse Distance Power Law Singularities” and “Physical Singularities” exist in the universe; including the “Big Bang Singularity”. “Physical Singularities” exists within spherical Black Hole Event Horizons enclosures.
|
Yes. I agree
|
|
Aphorism 1.6
Weak Cosmic Censorship
|
The Weak Cosmic Censorship claims or conjectures that no “Naked Singularities” can exist in nature, other than the “Big Bang Singularity”. Only “Physical Singularities” exists within Black Hole Event Horizons enclosures; the only exception is the “Big Bang Singularity”.
|
Yes. I agree
|
|
Aphorism 1.7
Cosmic “Conundrum” Censorship
|
The Cosmic “Conundrum” Censorship claims or conjectures that “Inverse Distance Power Law Singularities” describe infinitely large values ( ), and the “Physical Singularities” ( ), and the “Physical Singularities” ( ) describe infinitely small values, and the “Naked Singularities” ( ) describe infinitely small values, and the “Naked Singularities” (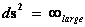 ) describe infinitely large values, of space, space-time, gravitational field, or the electrostatic field, in the same location of zero radius ( ) describe infinitely large values, of space, space-time, gravitational field, or the electrostatic field, in the same location of zero radius (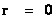 ); what are the implications? Is the singularity measurable? ); what are the implications? Is the singularity measurable?
|
I agree. But, I will add that I don’t think that singularities are actually measurable.
|
|
Aphorism 1.8
Strong Cosmic Censorship
|
The Strong Cosmic Censorship claims or conjectures that that General Relativity “Metric” Theory ( ) is a measurable and deterministic theory ( ) is a measurable and deterministic theory (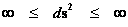 ), and is predictable from all data, including the initial data with zero radius ( ), and is predictable from all data, including the initial data with zero radius (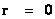 ) and would continue to be predictable with all other radius values, including final data at infinite radius ( ) and would continue to be predictable with all other radius values, including final data at infinite radius (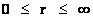 ). ).
|
No. I disagree.
|
|
Aphorism 1.9
Strong Cosmic “Most Probable” Censorship
|
The Strong Cosmic “Most Probable” Censorship claims or conjectures that that General Relativity “Metric” Theory (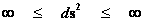 ) is a completely measurable and deterministic theory, only within a certain range, and is not predictable from the initial data, with zero radius ( ) is a completely measurable and deterministic theory, only within a certain range, and is not predictable from the initial data, with zero radius (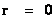 ), and the final data, where radius equals to infinity ( ), and the final data, where radius equals to infinity (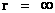 ), and would only be predictable and deterministic, with all other radius values, between the initial and final input values ( ), and would only be predictable and deterministic, with all other radius values, between the initial and final input values (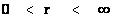 ). ).
|
Yes. I agree.
|
|
Aphorism 1.10
Strong “Coordinate Singularity” Censorship
|
The Strong “Coordinate Singularity” Censorship claims or conjectures that the “Coordinate Singularity” located at the Schwarzschild Radius (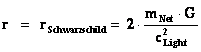 ) is a mathematical anomaly, and can be eliminated with proper mathematical resolution; thereby making the General Relativity “Schwarzschild Metric” Theory ( ) is a mathematical anomaly, and can be eliminated with proper mathematical resolution; thereby making the General Relativity “Schwarzschild Metric” Theory ( ) measurable, and predictable, at the Black Hole Event Horizon. ) measurable, and predictable, at the Black Hole Event Horizon.
|
Yes. I agree. There are mathematical solutions to the coordinate singularity. I don’t know why they are not popular.
|
|
Aphorism 1.11
Cosmic “Particle Creation” Censorship
|
The Cosmic “Particle Creation” Censorship claims or conjectures that Physical, Naked, and Inverse Power Law Singularities, except for the Big Bang Singularity, can be created around condensing matter, or static charge; and likewise, can be annihilated in the form of heat radiation electromagnetic energy, back into the surrounding universe; therefore all singularities are present where there is rest mass.
|
Yes. I agree. I believe that a singularity is the result of condensing of matter in a gravity vortex.
|
|
Aphorism 1.12
Cosmic “Photon Energy” Censorship
|
The Cosmic “Photon Energy” Censorship claims or conjectures that propagating “Photons” of electromagnetic energy void of rest mass, have “Singularities” along every point of its wavelength; therefore, Propagating Photons do not have singularities of any kind.
|
Yes. I agree. It does not make sense that a photon has a singularity, because there are possible three or more centers for a photon.
|
|
Aphorism 1.13
Cosmic “Universal Constants” Censorship
|
The Cosmic “Universal Constants” Censorship claims or conjectures that independent of linear, curvilinear, or rotational motion of any frame of reference, all the “Universal Constants” (i.e. Speed of Light Constant ( ), Universal Gravitational Constant ( ), Universal Gravitational Constant (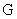 ), Planck’s Quantum of Action ( ), Planck’s Quantum of Action (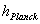 ) Constants, etc., are “Frame of Reference Invariant”, and remain the same everywhere in the universe, and in all frames of reference; and universal constants do not change over time, and have been the same, since the initial conditions at the very beginning of the Universe. ) Constants, etc., are “Frame of Reference Invariant”, and remain the same everywhere in the universe, and in all frames of reference; and universal constants do not change over time, and have been the same, since the initial conditions at the very beginning of the Universe.
|
Yes. I agree.
|
|
Aphorism 1.14
Cosmic “Universal Physical Law” Censorship
|
The Cosmic “Universal Physical Law” Censorship claims or conjectures that independent of linear, curvilinear, or rotational motion, or any location in the universe, all the “Universal Laws of Physics”, remain the same everywhere in the universe, and in all frames of reference.
|
Yes. I agree
|
|
Aphorism 1.15
Cosmic “Big Bang” Censorship
|
The Cosmic “Big Bang” Censorship claims or conjectures that the Universe has an origin, birth, or beginning initial state, known as the “Big Bang”, whose evolution and current state, can be described by predictable physics.
|
Yes. I agree
|
|
Aphorism 1.16
Cosmic “Immortal Existence” Censorship
|
The Cosmic “Immortal Existence” Censorship claims or conjectures that the Universe is Immortal, has always been, has always existed, and there is no “Big Bang”, origin of the universe, only current evolution and current state, can be described by predictable physics.
|
No. I disagree.
|
6. Appendix – 4 ─ Table of Universal Constants
Table of Universal Constants
|
Table of Universal Constants
|
|
Constant’s Name
|
Symbol
|
Constant Value
|
Units
|
|
Stephan Boltzmann’s Constant
|

|
5.670400474E-08
|
 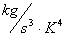
|
|
Boltzmann’s Energy Constant
|
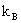
|
1.380650400E-23
|
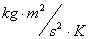
|
|
Speed of Light
|
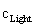
|
2.997924580E+08
|
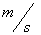
|
|
Planck’s Constant
|
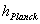
|
6.626068960E-34
|
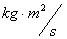
|
|
Universal Gravitational Constant
|
G
|
6.6742800E-11
|
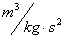
|
|
Black Hole Linear Mass Density
|

|
6.73297478332358E+26
|
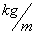
|
|
Dark Vacuum Force
|
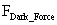
|
3.0256479774082E+43
|
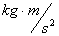
|
References
[1] The Nature of Space and Time, Steven Hawking (September 30, 1994) http://arxiv.org/pdf/hep-th/9409195v1.pdf
[2] Penrose Hawking Singularity Theorems
http://en.wikipedia.org/wiki/Penrose-Hawking_singularity_theorems
[3] Cosmic Censorship Hypothesis
http://en.wikipedia.org/wiki/Cosmic_censorship_hypothesis
[4] K.S. Thorne, “Validity in General Relativity of the Schwarzschild Criterion for Convection,” Astrophysical Journal, 144, 201-205 (1966)
[5] K. S. Thorne, “Warping Spacetime,” in The Future of Theoretical Physics and Cosmology: Celebrating Stephen Hawking’s 60th Birthday, edited by G.W. Gibbons, S.J. Rankin and E.P.S. Shellard (Cambridge University Press, Cambridge, England, 2003), Chapter 5, pp. 74-104; Chinese translation in Sixty Years in a Nutshell (Hunan Science and Technology Press, Hunan, China, 2005).
[6] Penrose, Roger: “The Question of Cosmic Censorship”, Chapter 5 in Black Holes and Relativistic Stars, Robert Wald (editor), (1994) (ISBN 0-226-87034-0)
[7] Penrose, Roger: “Singularities and time-asymmetry”, Chapter 12 in General Relativity: An Einstein Centenary Survey (Hawking and Israel, editors), (1979), see especially section 12.3.2, pp. 617–629 (ISBN 0-521-22285-0)
[8] Kruskal Szekeres Coordinates
http://en.wikipedia.org/wiki/Kruskal%E2%80%93Szekeres_coordinates
[9] Encyclopedia of Distance – (Kruskal-Szekeres Coordinates), Michel Marie Deza and Elena Deza, (Second Edition 2013) – Springer – ISBN 978-3-642-30958-8, Library of Congress Control Number 2012951148
[10] An Introduction to Black Holes, Sanjeev S. Seahra (February 6, 2006)http://www.math.unb.ca/~seahra/resources/notes/black_holes.pdf
[11] Physical Acceptability of Isolated, Static, Spherically Symmetric, Perfect Fluid Solutions of Einstein’s Equations, M.S.R. Delgaty and Kayll Lake1, Department of Physics, Queen’s University, Kingston Ontario, Canada K7L 3N6 (Dated: Septem 1998): http://arxiv.org/pdf/gr-qc/9809013v1.pdf
[12] Generating perfect fluid spheres in general relativity, Petarpa Boonserm, ∗ Matt Visser, and Silke Weinfurtner, School of Mathematics, Statistics, and Computer Science, Victoria University of Wellington,PO Box 600, Wellington, New Zealand (Dated: March 2005 – February 6, 2008): http://arxiv.org/pdf/gr-qc/0503007v1.pdf – (Pages: 13 – 16)
[13] Karl Friedrich Gauss, General Investigations of Curved Surfaces of 1827 and 1825, The Project Gutenberg EBook of General Investigations of Curved Surfaces of 1827 and 1825, by Karl Friedrich Gauss: http://www.gutenberg.org/files/36856/36856-pdf.pdf
[14] Gauss Law – Theorema Egregium:
http://en.wikipedia.org/wiki/Theorema_Egregium
[15] List of Differential Geometry Topics (Wikipedia): http://en.wikipedia.org/wiki/List_of_differential_geometry_topics
[16] D.F. Lawden. Introduction to Tensor Calculus, Relativity and Cosmology; Dover Publications; 3 edition (January 27, 2003), ISBN 978-0486425405 pp. 6-10
[17] Minkowski, Hermann (1907/8), “Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern“, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse: 53–111 *** Wikisource translation: The Fundamental Equations for Electromagnetic Processes in Moving Bodies.
[18] Einstein’s Paper: “Explanation of the Perihelion Motion of Mercury from General Relativity Theory”; Anatoli Andrei Vankov; IPPE, Obninsk, Russia; Bethany College, KS, USA:
[19] Schwarzschild, K. (1916). “Über das Gravitationsfeld eines Massenpunktes nach der Einstein’schen Theorie”. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften 1: 189–196: text of the original paper, in Wikisource:
[20] Schwarzschild Geodesics:
http://en.wikipedia.org/wiki/Schwarzschild_geodesics
[21] Robert Louis Kemp. “Super Principia Mathematica – The Rage To Master Conceptual & Mathematical Physics – The General Theory of Relativity.” ISBN 978-0-9841518-2-0, Flying Car Publishing Company, July 2010, pp. 20-21.
[22] Inertial-Mass-Vortex-Gravitation-Theory-Continued-Part-3, Robert Louis Kemp (2011). “Super Principia Mathematica – The Rage To Master Conceptual & Mathematical Physics, Flying Car Publishing Company
[23] Total-Mechanical-Energy-Conservation-Escape-Velocity-Binding-Energy-Einstein-Field-Equation, Robert Louis Kemp (2012). “Super Principia Mathematica – The Rage To Master Conceptual & Mathematical Physics
[24] A-Theory-Of-Gravity-For-The-21st-Century-The-Gravitational-Force-And-Potential-Energy-In-Consideration-With-Special-Relativity-General-Relativity, Robert Louis Kemp (2012). “Super Principia Mathematica – The Rage To Master Conceptual & Mathematical Physics
[24] Newtonian-Self-Gravitational-Force-Video-Lecture, Robert Louis Kemp (2012). “Super Principia Mathematica – The Rage To Master Conceptual & Mathematical Physics
[26] Conditions-For-The-Absence-And-Presence-Of-Matter-In-General-Relativity-Gr-Einstein-Field-Equations-Efes, Robert Louis Kemp (2012). “Super Principia Mathematica – The Rage To Master Conceptual & Mathematical Physics
[27] What-Are-The-Mathematical-And-Physical-Concepts-Of-Flat-Euclidean-And-Curved-Non-Euclidean-Gravitational-Fields, Robert Louis Kemp (2013). “Super Principia Mathematica – The Rage To Master Conceptual & Mathematical Physics
[28] The-Perfect-Fluid-Vacuum-Unified-Gravitation-Vortex-Model-And-Non-Euclidean-Spherically-Symmetric-Metrics, Robert Louis Kemp (2013). “Super Principia Mathematica – The Rage To Master Conceptual & Mathematical Physics
[29] Algorithm For Describing Spherically-Symmetric Metrics Of A Gravitational Field – Using-Space-Time-Angle-Metric-Components-Metric-Coefficients, Robert Louis Kemp (2013). “Super Principia Mathematica – The Rage To Master Conceptual & Mathematical Physics

















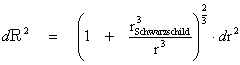




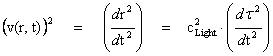










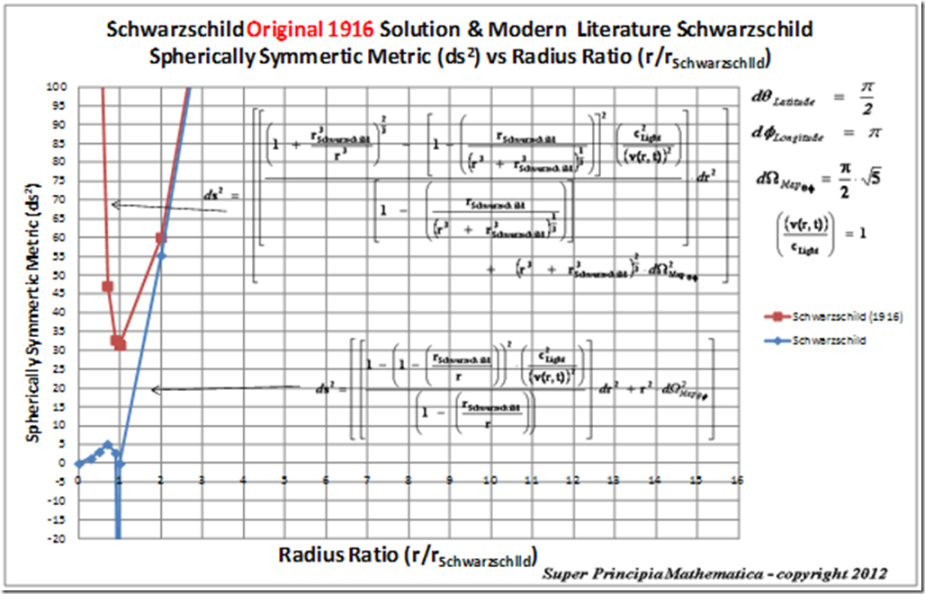
































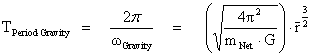
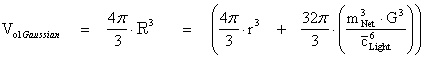















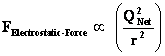
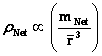
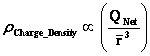
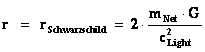

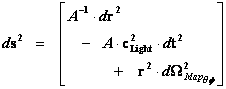





![clip_image002[17] clip_image002[17]](https://superprincipia.files.wordpress.com/2013/03/clip_image00217_thumb.gif?w=349&h=138)

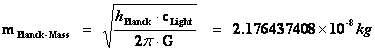

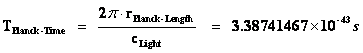



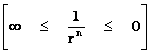


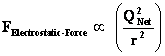
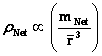
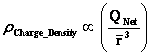
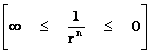
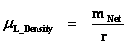

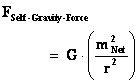

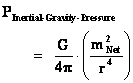
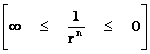
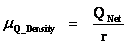
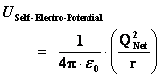


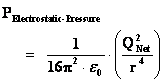
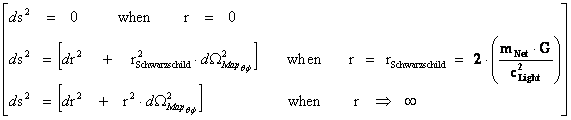

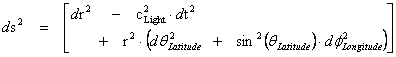
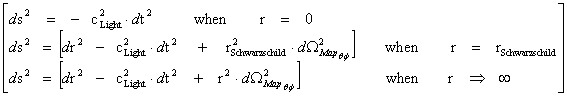



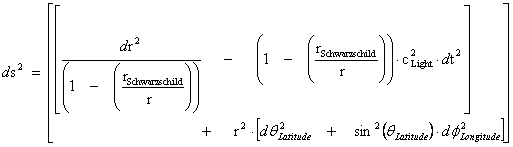
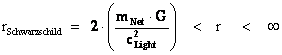
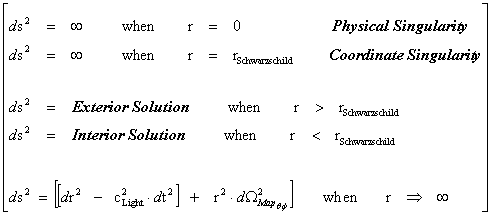


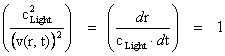


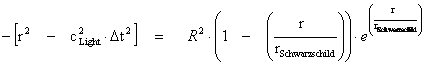
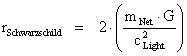

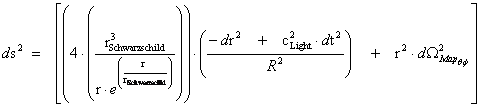
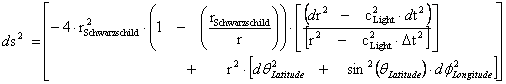
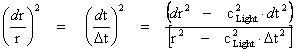
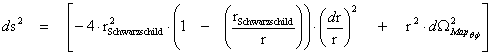
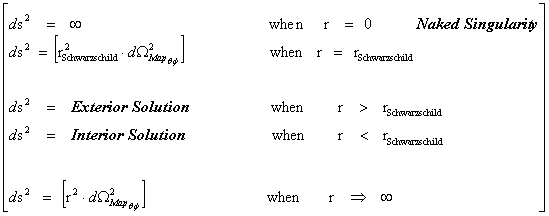

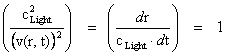







![clip_image002[6] clip_image002[6]](https://superprincipia.files.wordpress.com/2013/03/clip_image0026_thumb.gif?w=363&h=142)

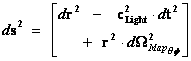



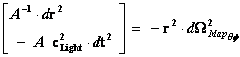
![clip_image002[21] clip_image002[21]](https://superprincipia.files.wordpress.com/2013/03/clip_image00221_thumb.gif?w=343&h=138)
![clip_image002[23] clip_image002[23]](https://superprincipia.files.wordpress.com/2013/03/clip_image00223_thumb.gif?w=355&h=102)



![clip_image002[25] clip_image002[25]](https://superprincipia.files.wordpress.com/2013/03/clip_image00225_thumb.gif?w=323&h=131)

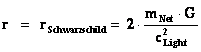













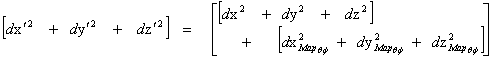



























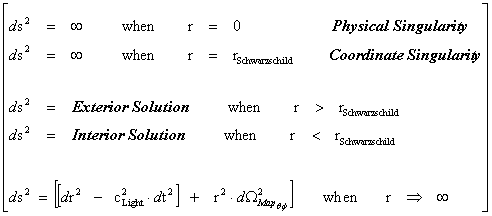
















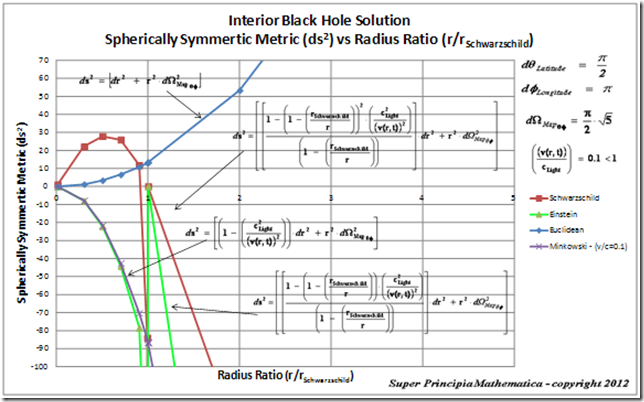







































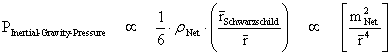





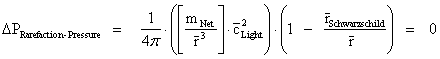


















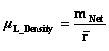





















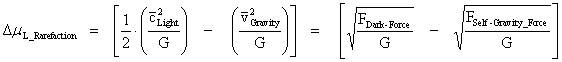






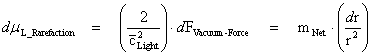








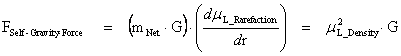
































































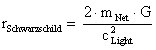



 ->
->